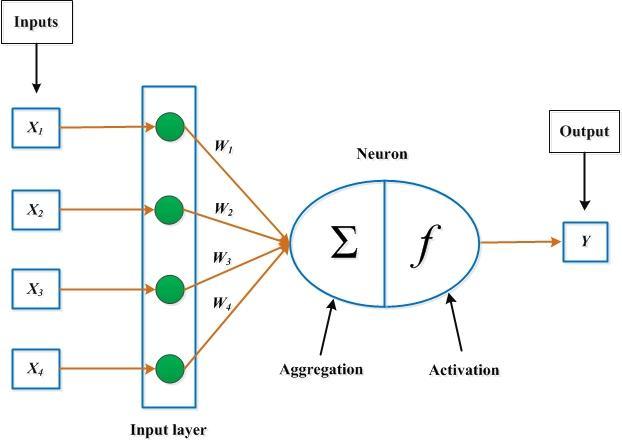
所谓激活函式(Activation Function),就是在人工神经网路的神经元上运行的函式,负责将神经元的输入映射到输出端。
基本介绍
- 中文名:激活函式
- 外文名:Activation Function
- 领域:神经网路
什幺是激活函式
激活函式(Activation functions)对于人工神经网路模型去学习、理解非常複杂和非线性的函式来说具有十分重要的作用。它们将非线性特性引入到我们的网路中。如图1,在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函式,这个函式就是激活函式。引入激活函式是为了增加神经网路模型的非线性。没有激活函式的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。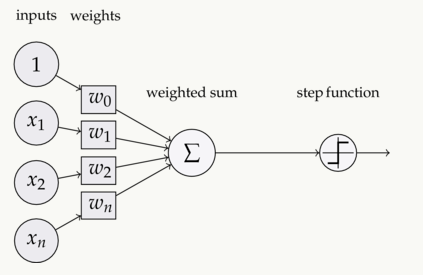 图1
图1
 图1
图1为什幺要用激活函式
如果不用激活函式,每一层输出都是上层输入的线性函式,无论神经网路有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函式给神经元引入了非线性因素,使得神经网路可以任意逼近任何非线性函式,这样神经网路就可以套用到众多的非线性模型中。
常用的激活函式
Sigmoid函式
Sigmoid函式是一个在生物学中常见的S型函式,也称为S型生长曲线。在信息科学中,由于其单增以及反函式单增等性质,Sigmoid函式常被用作神经网路的阈值函式,将变数映射到0,1之间。公式如下
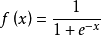
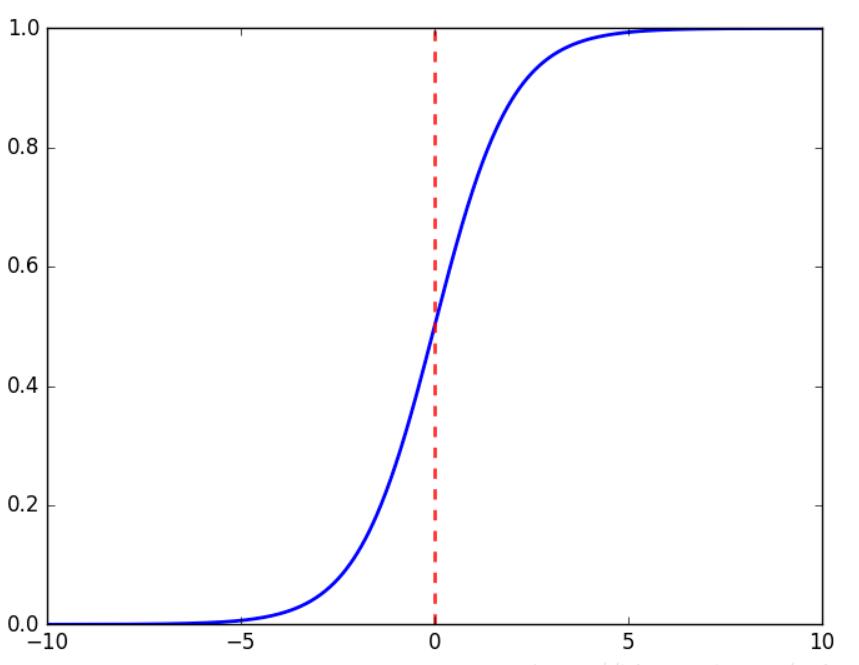 Sigmoid 图像
Sigmoid 图像Tanh函式
Tanh是双曲函式中的一个,Tanh()为双曲正切。在数学中,双曲正切“Tanh”是由基本双曲函式双曲正弦和双曲余弦推导而来。公式如下
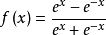
函式图像如下
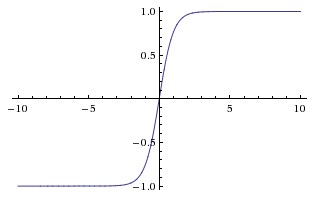 Tanh函式图像
Tanh函式图像ReLU函式
Relu激活函式(The Rectified Linear Unit),用于隐层神经元输出。公式如下
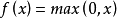
函式图像如下
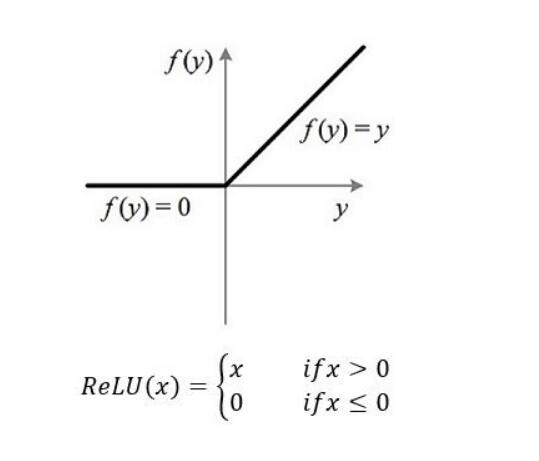 ReLU函式图像
ReLU函式图像
 ReLU函式图像
ReLU函式图像