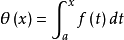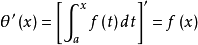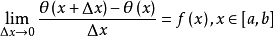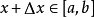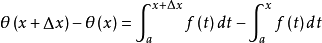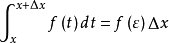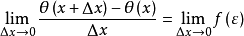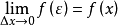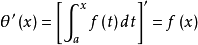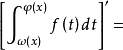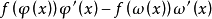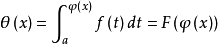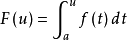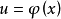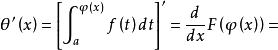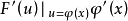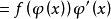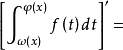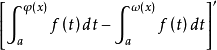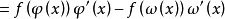原函式存在定理为:若f(x)在[a,b]上连续,则必存在原函式。此条件为充分条件，而非必要条件。即若f（x）存在原函式，不能推出f(x)在[a,b]上连续。由于初等函式在有定义的区间上都是连续的，故初等在其定义区间上都有原函式。需要注意的是初等函式的导数是一定是初等函式，初等函式的原函式不一定是初等函式。
基本介绍
- 中文名：原函式存在定理
- 外文名：Existence Theorem of Primitive Functions
- 学科：数学
- 解释：存在定理为:若f(x)在[a,b]上连续
定理内容
设f（x）在[a,b]上连续，则变上限积分
在[a,b]上可导，且其导数
定理证明
由导数定义，只需证明
设x∈(a，b），给x一个改变数△x，使
则
由积分中值定理，有
其中ε介于x与x+△x之间，因△x正负未知，不确定x与x+△x的大小。
等式两端除以△x，令△x→0，取极限
当△x→0时，x+△x→x，从而ε→x，又f（x）在[a,b]上连续，
所以，
该定理表明，设f（x）在[a,b]上连续，则必存在原函式且原函式为f（x）的变上限积分。
推论
设f（x）在[a,b]上连续，φ（x），ω（x）在[α,β]上可导，a≤φ﹙x﹚≤b,a≤ω（x）≤b，x∈[a,b].
则
证
它是由
与
的複合而成的函式，由複合函式微分法和原函式存在定理，且φ（x）在[α,β]上可导
又ω（x）在[α,β]上可导，a≤ω（x）≤b
原函式存在与间断点的关係
设F'（x）=f(x)，f（x）在x=x0处不连续，则x0必为第二类间断点（对于考研数学，只能是第二类振荡间断点），而非第一类间断点或第二类无穷间断点。
当f(x)存在第二类振荡间断点时，不能确定是否存在原函式，这种情况下结论与f(x)的表达式有关。
原函式存在的三个结论：
如果f(x)连续，则一定存在原函式；
如果f(x)不连续，有第一类可去、跳跃间断点或第二类无穷间断点，那幺包含此间断点的区间内，一定不存在原函式；
如果f(x)不连续，有第二类振荡间断点，那幺包含此间断点的区间内，原函式可能存在，也可能不存在。
