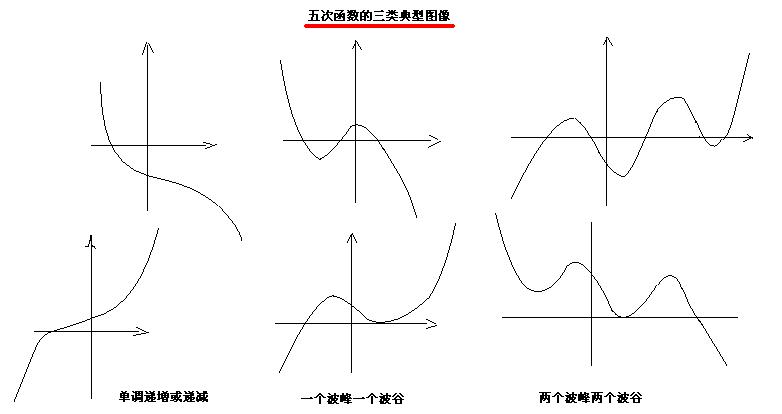
一般的,形如f(x)=ax5+bx4+cx3+dx2+ex+f(a≠0)的函式叫作五次函式。a、b、c、d、e、f对应为其的五、四、三、二、一次项係数与常数。
基本介绍
- 中文名:五次函式
- 定义域:R
- 值域:R
- 单调性:根据函式解析式而变换
- 周期性:无周期
- 奇偶性:无
基本定义
一般的,自变数x和因变数y存在如下关係:y=ax^5+bx^4+cx^3+dx^2+ex+f的函式,称y为x的五次函式。其中,a、b、c、d、e分别为五次、四次、三次、二次、一次项係数,f为常数,a≠0。在实际中,一般不使用此函式。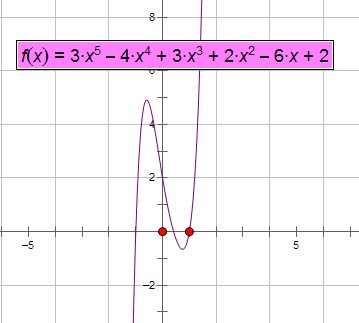 五次函式
五次函式
 五次函式
五次函式求解方法
一般的五次方程没有统一的公式解存在。 Clone于2009年寒假在山东省潍坊市市委党校跟江西省数学会副会长陶平生先生讨论五次方程是否有公式解的时候,陶平生先生否定有统一的公式解一说。陶平生先生认为:群论是解决该问题的一种很好的方法。其实,在我们的人教B版高中数学课本《选修3-4对称与群》里,已经说明:第一,1824年:挪威的一位年轻人阿贝尔证明了:五次代数方程通用的求根公式是不存在的;第二,伽罗瓦证得了5次及其以上方程没有统一的求根公式;第三,伽罗瓦能给出恰好有H=Sn的方程,而在群论里面很容易证明当n≥5时,Sn不是一个可解群 。但可以用二分法近似的求出方程的解。
五次函式f(x)=ax^5+bx^4+cx^3+dx^2+ex+f其导数为f‘(x)=5ax^4+4bx^3+3cx^2+2dx+e,对于其导数,我们可以对函式进行求极值点与求其单调区间。