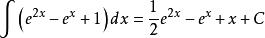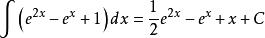在微积分中，一个函式f 的不定积分，或原函式，或反导数，是一个导数等于f 的函式 F ，即F ′ = f。
不定积分和定积分间的关係由微积分基本定理确定。其中F是f的不定积分。
基本介绍
- 中文名：不定积分
- 外文名：indefinite integral
- 本质：函式表达式
- 类别：高等数学
- 符号：∫
- 套用学科：微积分
解释
根据牛顿-莱布尼茨公式，许多函式的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关係：定积分是一个数，而不定积分是一个表达式，它们仅仅是数学上有一个计算关係。一个函式，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。连续函式，一定存在定积分和不定积分；若在有限区间[a,b]上只有有限个间断点且函式有界，则定积分存在；若有跳跃、可去、无穷间断点，则原函式一定不存在，即不定积分一定不存在。
性质
1、函式的和的不定积分等于各个函式的不定积分的和；即：设函式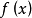
及
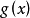的原函式存在，则
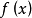
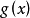
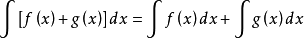
2、求不定积分时，被积函式中的常数因子可以提到积分号外面来。即：设函式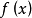的原函式存在，
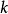非零常数，则
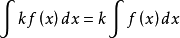
求解
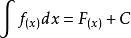
由定义可知：
求函式f(x)的不定积分，就是要求出f(x)的所有的原函式，由原函式的性质可知，只要求出函式f(x)的一个原函式，再加上任意的常数C就得到函式f(x)的不定积分。
积分公式
注：以下的C都是指任意积分常数。
1、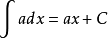
，a是常数
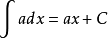
2、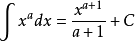
，其中a为常数，且a ≠ -1
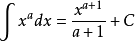
3、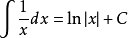
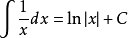
4、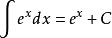
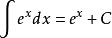
5、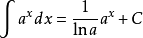
，其中a > 0 ，且a ≠ 1
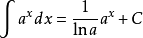
6、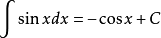
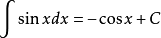
7、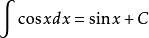
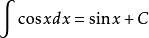
8、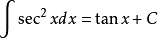
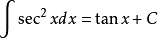
9、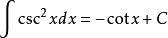
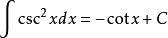
10、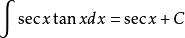
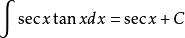
11、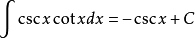
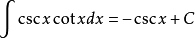
12、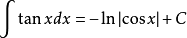
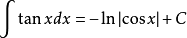
13、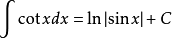
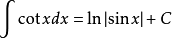
14、
15、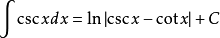
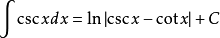
全体原函式之间只差任意常数C
证明：如果f(x)在区间I上有原函式，即有一个函式F(x)使对任意x∈I，都有F'(x)=f(x)，那幺对任何常数显然也有[F(x)+C]'=f(x).即对任何常数C，函式F(x)+C也是f(x)的原函式。这说明如果f(x)有一个原函式,那幺f(x)就有无限多个原函式。
不定积分
不定积分设G(x)是f(x)的另一个原函式,即∀x∈I，G'(x)=f(x)。于是[G(x)-F(x)]'=G'(x)-F'(x)=f(x)-f(x)=0。
由于在一个区间上导数恆为零的函式必为常数，所以G(x)-F(x)=C’(C‘为某个常数)。
这表明G(x)与F(x)只差一个常数.因此,当C为任意常数时，表达式F(x)+C就可以表示f(x)的任意一个原函式。也就是说f(x)的全体原函式所组成的集合就是函式族{F(x)+C|-∞<C<+∞}。
由此可知，如果F(x)是f(x)在区间I上的一个原函式，那幺F(x)+C就是f(x)的不定积分，即∫f(x)dx=F(x)+C。
因而不定积分∫f(x) dx可以表示f(x)的任意一个原函式。
积分方法
积分公式法
直接利用积分公式求出不定积分。
换元积分法
换元积分法可分为第一类换元法与第二类换元法。
不定积分
不定积分一、第一类换元法（即凑微分法）
通过凑微分，最后依託于某个积分公式。进而求得原不定积分。例如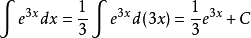
。
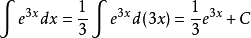
二、注：第二类换元法的变换式必须可逆，并且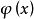
在相应区间上是单调的。
第二类换元法经常用于消去被积函式中的根式。当被积函式是次数很高的二项式的时候，为了避免繁琐的展开式，有时也可以使用第二类换元法求解。常用的换元手段有两种：
1、 根式代换法，
2、 三角代换法。
在实际套用中，代换法最常见的是链式法则，而往往用此代替前面所说的换元。
链式法则是一种最有效的微分方法，自然也是最有效的积分方法，下面介绍链式法则在积分中的套用：
链式法则：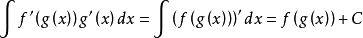
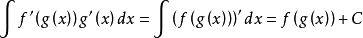
我们在写这个公式时，常常习惯用u来代替g，即：
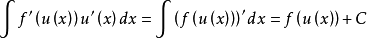
如果换一种写法，就是让：
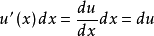
就可得：
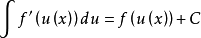
分部积分法
设函式和u，v具有连续导数，则d(uv)=udv+vdu。移项得到udv=d(uv)-vdu
不定积分
不定积分两边积分，得分部积分公式
∫udv=uv-∫vdu。 ⑴
称公式⑴为分部积分公式．如果积分∫vdu易于求出，则左端积分式随之得到．
分部积分公式运用成败的关键是恰当地选择u,v
一般来说，u,v 选取的原则是：
1、积分容易者选为v， 2、求导简单者选为u。
例子：∫Inx dx中应设U=Inx,V=x
分部积分法的实质是：将所求积分化为两个积分之差，积分容易者先积分。实际上是两次积分。
有理函式分为整式（即多项式）和分式（即两个多项式的商），分式分为真分式和假分式，而假分式经过多项式除法可以转化成一个整式和一个真分式的和．可见问题转化为计算真分式的积分．
可以证明，任何真分式总能分解为部分分式之和。
不可积函式
虽然很多函式都可通过如上的各种手段计算其不定积分，但这并不意味着所有的函式的原函式都可以表示成初等函式的有限次複合，原函式不可以表示成初等函式的有限次複合的函式称为不可积函式。利用微分代数中的微分Galois理论可以证明，如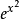
，xx ，sinx/x这样的函式是不可积的。
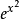
不定积分
不定积分积分表
含有三角函式的积分
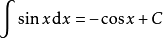
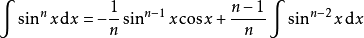
示例
例1 求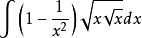
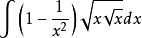
解：原式=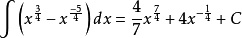
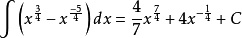
例2 求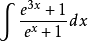
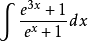
解：原式=
