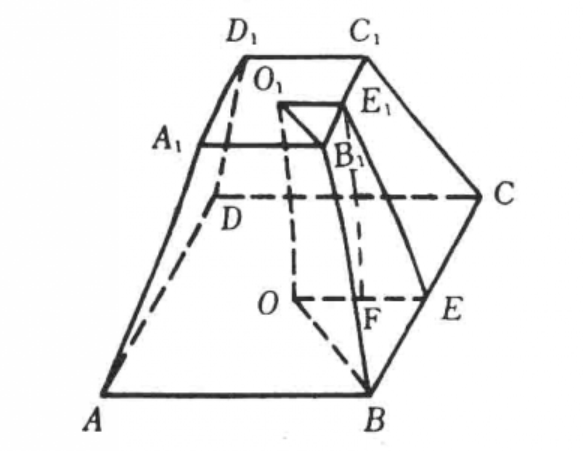
正稜台(regular prismoid)是一种特殊的稜台,是由正稜锥截得的稜台。正稜台的两底面是两个相似正多边形,侧面是全等的等腰梯形,中国古算书上把正四稜台称为方亭或方台。
基本介绍
- 中文名:正稜台
- 外文名:regular prismoid
- 所属学科:数学
- 所属问题:立体几何(多面体)
- 简介:由正稜锥截得的稜台
基本概念
用一个平行于稜锥底面的平面去截稜锥,介于底面和截面之间的部分叫做稜台(图1)。其各部分的名称如图2所示。由正稜锥截得的稜台叫做正稜台。
正稜台的主要性质
正稜台的主要性质有:
1.正稜台的两底面以及平行于底面的截面是相似正多边形;
2.各侧棱都相等;
3.侧面是全等的等腰梯形;
4.斜高都相等;
5.对角面是等腰梯形;
6.两底面中心的连线垂直于底面;
7.各侧棱和底面所成的角相等;
8.各侧面和底面所成的二面角相等。
正稜台的侧面展开图
正稜台的侧面展开图图3(b)是由各个侧面组成的平面图形,它是由一些有公共顶点的等腰梯形组成的,这个公共顶点即为等腰梯形两腰延长后的交点。等腰梯形的上、下底就是正稜台上、下底面边长.等腰梯形的腰就是正稜台的侧棱长。
正稜台的表面积
图3是正稜台和它的侧面展开图,这个侧面展开图是由几个全等的等腰梯形组成的,每个梯形的上底和下底分别是正稜台上底面和下底面多边形的边,两腰是正稜台的侧棱,设这个正稜台上、下底面周长分别是c'和c,斜高是h',我们有下面的定理:
定理 正稜台的侧面积等于它的两个底面周长的和与斜高的乘积的一半,即
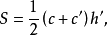
 图3(a)
图3(a)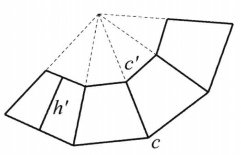 图3(b)
图3(b)正稜台的体积
设稜台的上底面积为S1,下底面积为S2,高为h,它的体积为V,则稜台的体积计算公式如下:
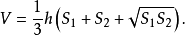
稜台的体积等于这三个稜锥的体积之和:
1.以稜台的高作高,它的下底作底的;
2.以稜台的高作高,它的上底作底的;
3.以稜台的高作高,它的上下两底面积的比例中项作底的。