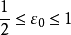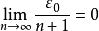积分第一中值定理是积分中值定理的推广之一,此外还有积分第二中值定理。积分中值定理揭示了一种将积分化为函式值, 或者是将複杂函式的积分化为简单函式的积分的方法。是数学分析的基本定理和重要手段, 在求极限、判定某些性质点、估计积分值等方面套用广泛。
基本介绍
- 中文名:积分第一中值定理
- 外文名:First mean value theorem for definite integrals
- 别称:First Integration Mid-value Theorem
- 套用学科:数学
- 适用领域範围:微积分
定理定义
如果函式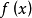 在闭区间
在闭区间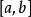 上连续,
上连续,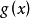 在
在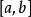 上不变号,并且
上不变号,并且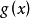 在闭区间
在闭区间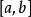 上是可积的,则在
上是可积的,则在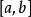 上至少存在一个点
上至少存在一个点 ,使下式成立:
,使下式成立:
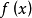
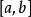
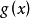
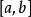
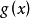
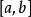
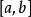

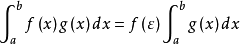
定理证明
由于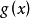 在
在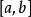 上不变号,不妨设
上不变号,不妨设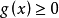 。并且由
。并且由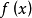 在
在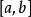 上的连续性可知,
上的连续性可知,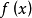 在
在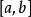 上存在最大值
上存在最大值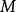 和最小值
和最小值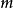 ,使得
,使得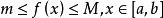 ,将不等式两边同时乘以
,将不等式两边同时乘以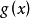 ,得到:
,得到:
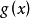
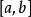
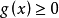
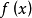
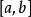
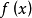
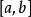
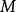
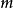
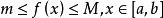
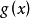
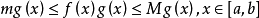
,对上式在上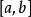 取积分得
取积分得
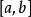
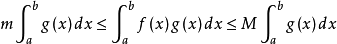
若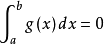 ,上式等号成立,
,上式等号成立,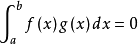 ,定理显然成立。
,定理显然成立。
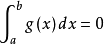
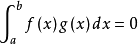
若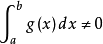 ,不等式两边同除以
,不等式两边同除以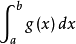 ,有
,有
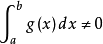
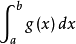
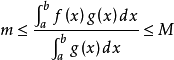
由介值定理,存在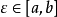 ,使得
,使得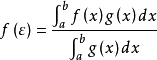 ,即
,即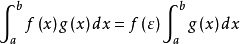 。定理得证。
。定理得证。
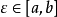
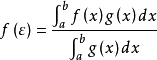
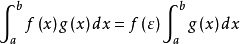
套用实例
求极限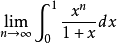 。
。
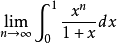
解:取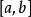 为
为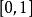 ,
,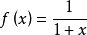 ,
,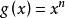 ,则
,则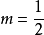 ,
,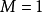 ,并有
,并有
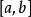
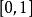
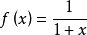
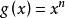
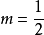
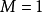

由于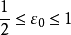 有界,因此
有界,因此