积分中值定理分为积分第一中值定理和积分第二中值定理,它们各包含两个公式。积分中值定理揭示了一种将积分化为函式值, 或者是将複杂函式的积分化为简单函式的积分的方法, 是数学分析的基本定理和重要手段, 在求极限、判定某些性质点、估计积分值等方面套用广泛。但是其闭区间的鬆弛,导致在其闭区间端点处点的讨论存在限制,这里将讨论加强条件的积分中值定理,将其区间加强为开区间。
简介
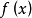
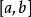
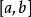

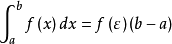
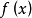
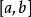
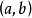

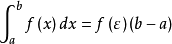
定理证明
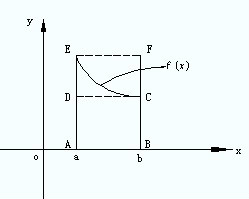
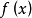
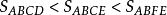
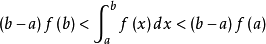
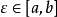
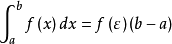
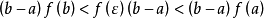
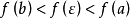
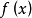
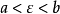
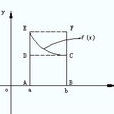
积分中值定理分为积分第一中值定理和积分第二中值定理,它们各包含两个公式。积分中值定理揭示了一种将积分化为函式值, 或者是将複杂函式的积分化为简单函式的积分的方法, 是数学分析的基本定理和重要手段, 在求极限、判定某些性质点、估计积分值等方面套用广泛。但是其闭区间的鬆弛,导致在其闭区间端点处点的讨论存在限制,这里将讨论加强条件的积分中值定理,将其区间加强为开区间。
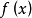
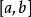
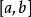

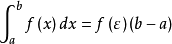
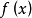
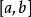
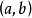

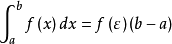

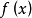
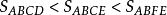
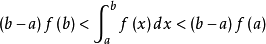
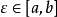
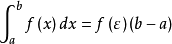
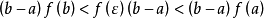
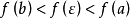
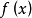
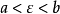
Powered By 种豆资源网||