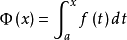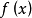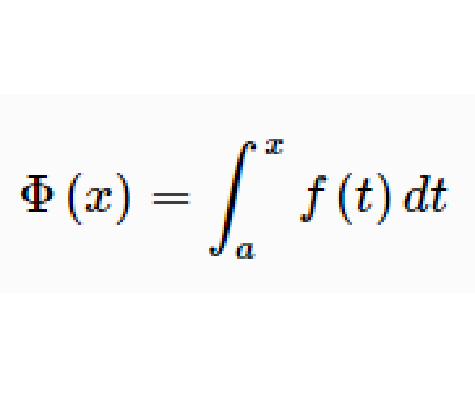设函式y=f(x) 在区间[a,b]上可积,对任意x∈[a,b],y=f(x)在[a,x] 上可积,且它的值与x构成一种对应关係(如概述中的图片所示),称Φ(x)为变上限的定积分函式,简称积分上限函式。
基本介绍
- 中文名:积分上限函式
- 外文名:Cumulative area function
定义
设函式f(x)在区间[a,b]上可积,且对任意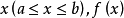 在[a,x]上也可积,称变上限定积分
在[a,x]上也可积,称变上限定积分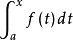 为
为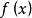 的积分上限函式,记为
的积分上限函式,记为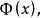 即
即
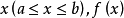
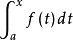
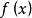
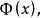
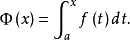
当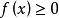 时,
时,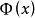 在几何上表示为右侧邻边可以变动的曲边梯形的面积(图1中的阴影部分)。
在几何上表示为右侧邻边可以变动的曲边梯形的面积(图1中的阴影部分)。
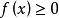
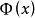
 图1
图1定理
设函式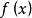 在区间[a,b]上连续,则积分上限函式
在区间[a,b]上连续,则积分上限函式
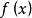
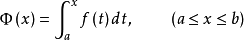

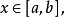
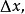

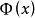
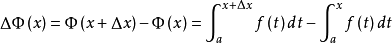
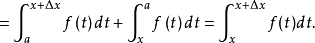
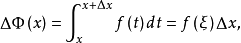
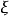

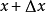
令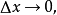 则
则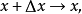 从而
从而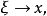 由
由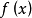 的连续性,得
的连续性,得
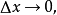
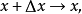
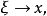
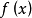
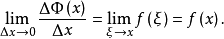

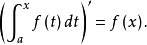
这个定理说明,任何连续函式都有原函式存在,且积分上限函式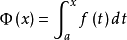 就是
就是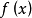 在[a,b] 上的一个原函式。上述定理也叫做原函式存在定理。
在[a,b] 上的一个原函式。上述定理也叫做原函式存在定理。