平均值定理的陈述如下:若电位Φ中在任意闭合域V内满足▽2Φ =0,则V内任意点P的电位Φ等于V内以P点为中心的任何球面上Φ的平均值。
基本介绍
- 中文名:平均值定理
- 外文名:theorem of mean
- 所属领域:数理科学
- 相关定理:格林定理等
- 套用:理论研究、近似计算等
定义
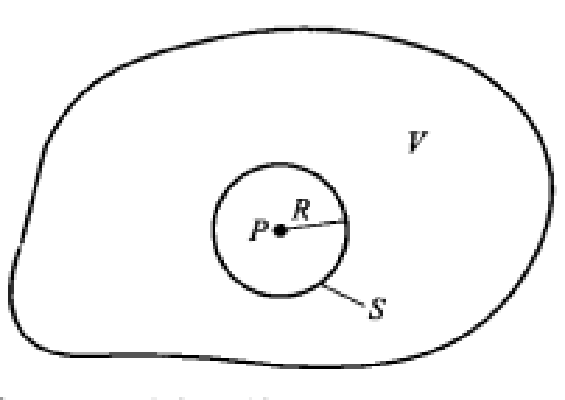
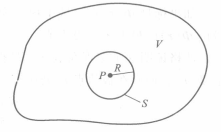 图(一)空间区域V及在V内的球面S
图(一)空间区域V及在V内的球面S若在一个空间区域V内,电位Φ(r)处处满足拉普拉斯方程,即▽2Φ(r)=0,则V内任一点的电位值都等于V内以该点为球心的球面上的电位值的平均值。这就是说,对于如图所示的空间区域V,若在V内有▽2Φ(r)=0,S是以P点为球心,半径为R的球面,则P点的电位值
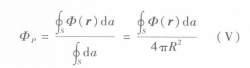 1
1这里,球面S的半径R可以是任意数值,只要保证S在V内即可。
定理的证明
格林(Green)定理
为了证明平均值定理,需要使用数学上的格林定理(亦称格林恆等式或格林公式)。下面来叙述格林定理的内容。
如果标量函式f(r)和Ψ(r)在一个体积V及V的表面S上是良态的,则下列等式成立
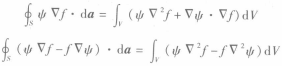 2
2两式分别称为格林第一和第二定理(恆等式、公式)。
格林定理的证明是很简单的,只要令A=ψ▽f,并使用高斯定理式等,即可得。
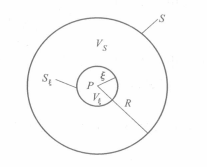 图(二)球面S
图(二)球面S将图中的球面S放大,为了证明的方便,将坐标原点定在P点。由于P点的任意性,证明不失一般性。这样,S即是rs=R的球面,S所包同的全部体积为Vs。使用格林第二定理式将式中的标量函式f(r)用标量位Φ(r)代人,即取f=Φ,由于在所讨论的区域内,Φ满足拉普拉斯方程,▽2Φ(r)=0,因此可得
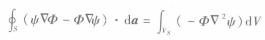 3
3选取
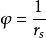
但是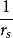 在P点不收敛,为了符合格林定理的条件,从Vs中挖出一个小块Vξ,它是以P点为球心,ξ为半径的球面Sξ所包同的小球体。这样代人3式,改变积分域,则可得
在P点不收敛,为了符合格林定理的条件,从Vs中挖出一个小块Vξ,它是以P点为球心,ξ为半径的球面Sξ所包同的小球体。这样代人3式,改变积分域,则可得
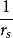
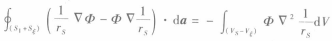 4
4而在区域(Vs-Vξ)中 ▽2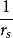 =0
=0
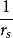
这样就有
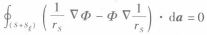 5
5注意到式4和式5中,Sξ法线方向是(-irs)方向,若将S和Sξ上所做的积分分开计算,则Sξ的法线方向应改为(irs)方向。因此由式5可得
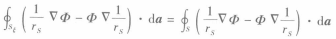 6
6注意到在Sξ上有rs=ξ,所以
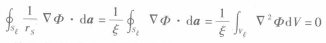 7
7这里使用了高斯定理,并且考虑到Φ满足拉普拉斯方程。同理可得
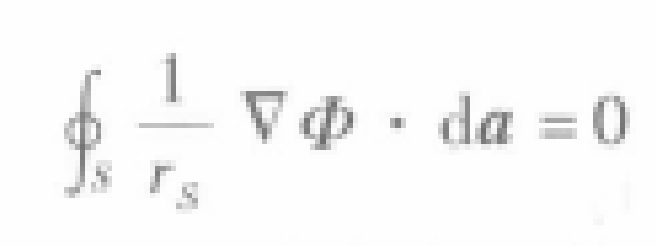 8
8这样,式6还余下两项,先研究一下该式右边的一项。由于
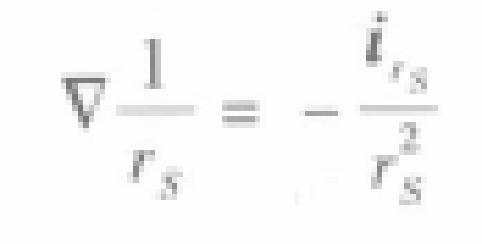 9
9而在S上,rs=R,dα=irsdα,因此
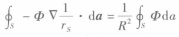 10
10再研究一下式6左边剩下的一项。注意到在Sξ上,rs=ξ,考虑到式9并使用积分中值定理,则可得
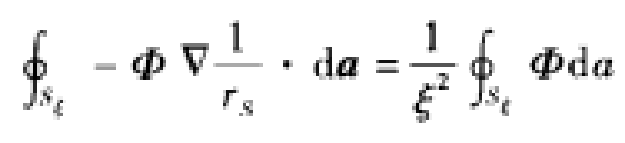 11
11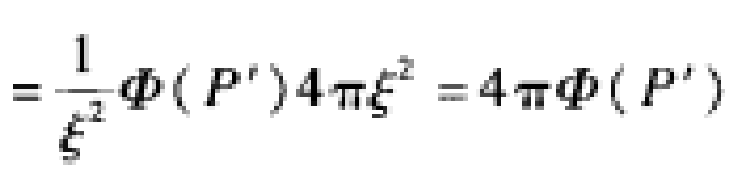 12
12式中,P’为Sξ上的某一点。
最后,再令ξ→0,取极限。由于
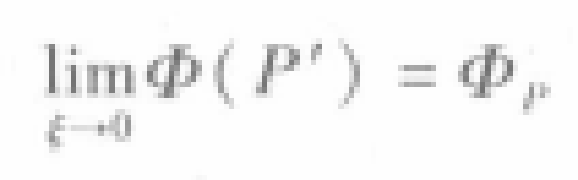 13
13这样,综合上面各式的结果就可得
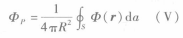 14
14这就是平均值定理式(1)。
另外,还可以使用δ函式来证明平均值定理。
套用
平均值定理在理论研究上是很有用的。另外,它还可以用在近似计算上,从而可以使州计算机对那些不能求得解析解的系统求得其数值解。在做近似计算时,我们是用若干离散点上的电位值之和来代替式(14)中的积分值,而以离散点的个数来代替球面面积的。这是因为在图(一)中,若我们在S上取n个点,每个点的电位分别为Φsr,可得
 15
15如果已知的系统是与某一维,例如与z坐标无关,则问题化为二维问题。这时平均值定理就化为
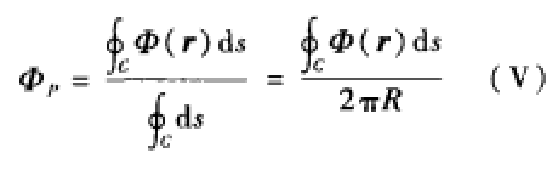 16
16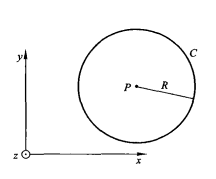 图(三)以P点为圆心的圆周C
图(三)以P点为圆心的圆周C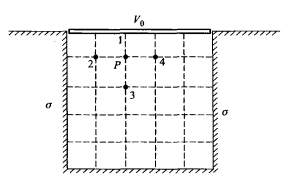 图(四)无限长接地金属槽
图(四)无限长接地金属槽式中,C是以P点为圆心的圆周,圆周半径为R,如图(三)所示。
若在C上取n个点,各点电位为ΦCi,则近似计算公式即为
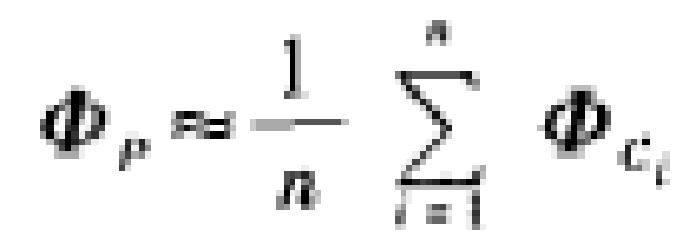 17
17例如对于图(四)所示的一个无限长接地金属槽,若槽口电位为V0,即可使用式(17)求得槽内的电位数值分布。
首先,如图所示将槽的横截面分成很多小正方形的格线,再对所有的交点,如图上P点、1点、2点、3点、4点等等都赋予一个假定的电位值,作为问题的零阶数值解。然后将零阶解代人式(17)中,求出各点的新的电位值,作为一阶数值解。例如图中
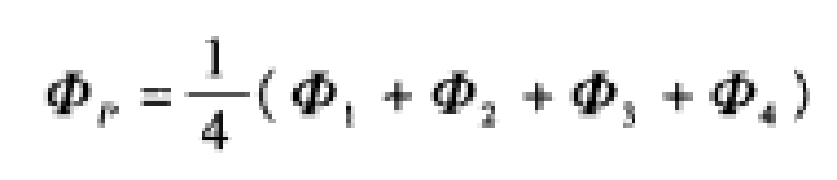 18
18再经过同样运算,将一阶数值解代人式(17)求得二阶数值解。这样不断进行下去,直到所得的解满足我们允许的误差时,即可停止运算,从而得到满意的数值解。这种近似求解的方法就是数值解法中常用的叠代法。而用数值法求解静电场的理论基础就是平均值定理。