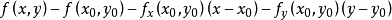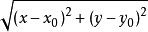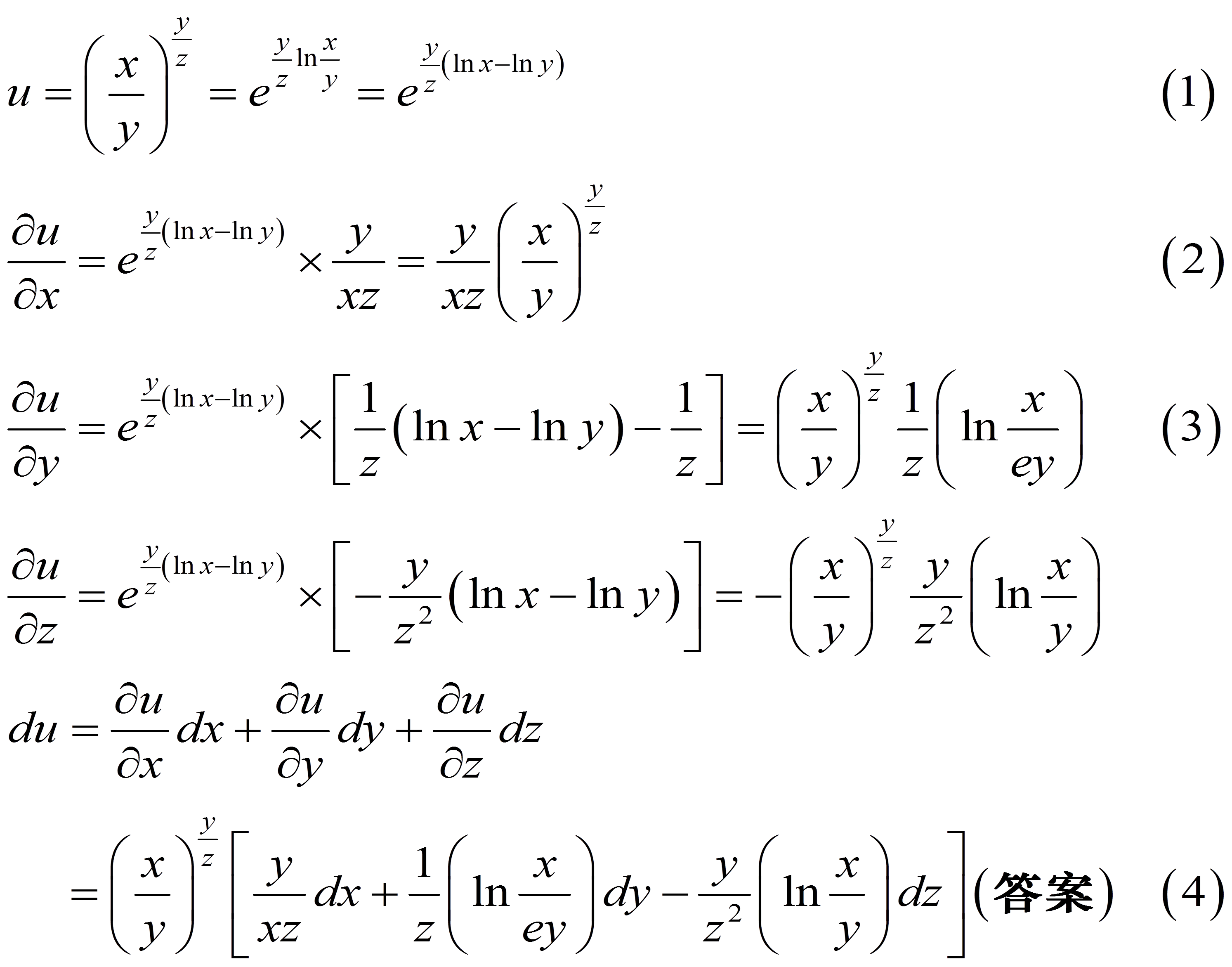如果函式z=f(x, y) 在(x, y)处的全增量
Δz=f(x+Δx,y+Δy)-f(x,y)
可以表示为
Δz=AΔx+BΔy+o(ρ),
其中A、B不依赖于Δx, Δy,仅与x,y有关,ρ趋近于0(ρ=√[(Δx)2+(Δy)2]),此时称函式z=f(x, y)在点(x,y)处可微分,AΔx+BΔy称为函式z=f(x, y)在点(x, y)处的全微分,记为dz即
dz=AΔx +BΔy
该表达式称为函式z=f(x, y) 在(x, y)处(关于Δx, Δy)的全微分。
基本介绍
- 中文名:全微分
- 外文名:total differential
- 函式:z=f(x, y)
- 学科:数学
- 公式:dz=fx(x,y)Δx+fy(x,y)Δy
- 相关名词:导数
全增量
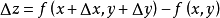
全微分
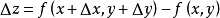
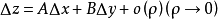
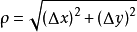
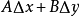
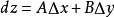
定理
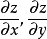
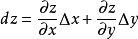
判别可微方法