弗雷歇微分简称F微分，亦称强微分，是数学分析中全微分概念和变分法中强变分概念的推广。

强可微的概念是由弗雷歇于1910年引入的。

设X,Y为赋范线性空间，Ω是X中的开集，f:Ω→Y是映射，x₀∈Ω。若存在有界线性运算元A:X→Y ,使得f(x₀+h)-f(x₀)-Ah=o(||h||)，其中o(||h||)/||h||→0(当||h||→0)，则称 f 在x₀弗雷歇可微（简称F可微）或强可微，A称为f在x₀的弗雷歇导运算元（简称F导运算元）或强导运算元，记为df(x₀)或f'(x₀)，Ah称为f在x₀沿h的F微分或强微分，记为df(x₀;h)或f'(x₀)h。

若f在几中每点均为F可微，则称f在Q上F可微。

f在x₀F可微蕴涵着f在x₀连续。

f在x₀F可微等价于f在x₀（有界线性）G可微且极限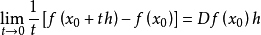关于||h||=1为一致的，F可微通常简称可微。