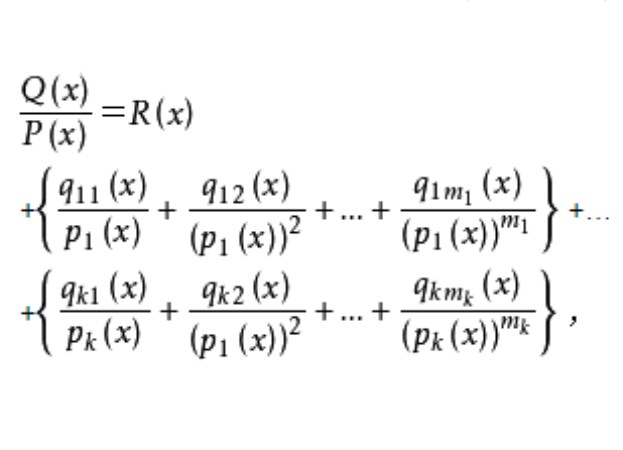有理函式是指由两个多项式函式的商所表示的函式，其一般形式为

其中n,m为非负整数，与都是常数，且。

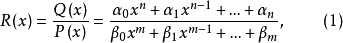
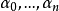
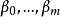
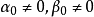
若m>n，则称它为真分式；若m≤n，则称它为假分式。由多项式的除法可知，假分式总能化为一个多项式与一个真分式之和。由于多项式的不定积分是容易求得的，因此只需研究真分式的不定积分，故设(1)为一有理真分式。

根据代数知识，有理真分式必定可以表示成若干个部分分式之和(称为部分分式分解)，因而问题归结为求那些部分分式的不定积分。

设需要求

其中P，Q都是多项式，如果Q的次数大于或等于P的次数，则先用除法分出商多项式R，设多项式P(x)在R上已分解为既约多项式之积：，p₁(x)，p₂(x)，…，p_k(x)为一次或二次多项式，则有：

=

+ +…

+ ，

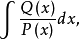
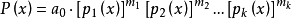
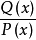
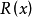
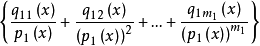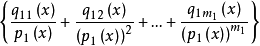
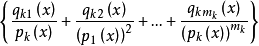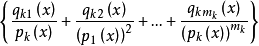
q_ij(i=1，2，…，k，j=1，2，…，m_k)是次数比p_i的次数低的多项式。对上式积分，右边出现三类积分：多项式的积分；形如

其中(a，A，k∈R)的积分；和形如

的积分。对第三类积分，改写Bx+C=(2x+p)·(B/2)+(C-pB/2)，

将它分解为两个积分

其中，第一个积分已可求出，对第二个积分，如m=1，则易于求出;如m>1，用分部积分法，得

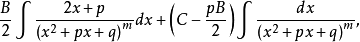
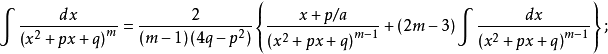
如m-1>1，则可再利用此公式，逐次递推，最后便可求出积分。