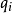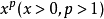积分不等式是微积分学中的一类重要不等式,也为解决微分方程等方面的问题提供了 富有成效的理论工具。主要有杨不等式,施瓦兹不等式,闵可夫斯基不等式,延森不等式等。
基本介绍
- 中文名:积分不等式
- 外文名:integral inequality
- 举例:杨不等式、施瓦兹不等式等
- 类型:数学术语
- 隶属:微积分学
杨不等式
有关函式及其反函式积分的不等式。设f在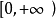 上连续,且严格增,
上连续,且严格增,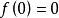 ,则对任意的a≥0及
,则对任意的a≥0及
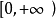
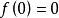
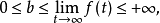
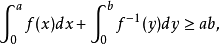
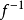
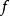
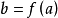
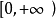
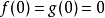
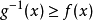
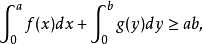
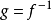
 图1杨不等式的几何意义
图1杨不等式的几何意义从杨不等式可以得到一些有用的不等式,如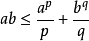 (也有人称为杨不等式),其中1/p+1/q=1,p>1,q>1,a,b≥0,等号若且唯若
(也有人称为杨不等式),其中1/p+1/q=1,p>1,q>1,a,b≥0,等号若且唯若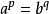 时成立。若f:
时成立。若f: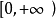 →
→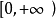 ,右连续且增,
,右连续且增,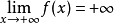 ,则f(x)称为杨函式。若对杨函式f(x),定义其右反函式
,则f(x)称为杨函式。若对杨函式f(x),定义其右反函式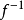 为:y∈[0,f(0)]时,
为:y∈[0,f(0)]时,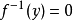 ;而
;而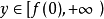 时,
时,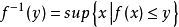 。则对a,b≥0,有
。则对a,b≥0,有
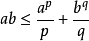
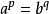
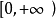
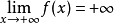
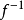
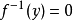
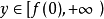
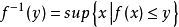
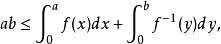
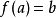
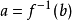
杨不等式可以推广(1989)为
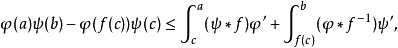
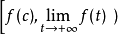
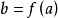
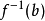
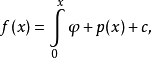
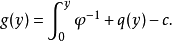
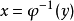
施瓦兹不等式
赫尔德不等式中用得最普遍的是p=q=2的情况,此时的赫尔德不等式称为施瓦兹不等式,有时也称为柯西不等式或布尼亚科夫斯基不等式。
见施瓦兹不等式。
闵可夫斯基不等式
(1)对所有的正实数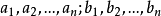 有
有
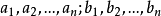
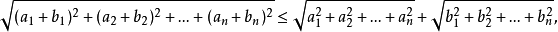
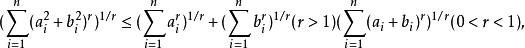
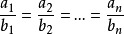
(2)设E为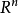 中的勒贝格可测集,f(x),g(x)为E上p次
中的勒贝格可测集,f(x),g(x)为E上p次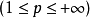 实值可积函式,则f(x)+g(x)是E上p次可积函式,并且:
实值可积函式,则f(x)+g(x)是E上p次可积函式,并且:
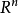
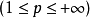

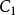
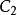
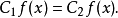
(3)序列形式的闵可夫斯基不等式。
设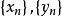 为两个实数列,满足条件
为两个实数列,满足条件
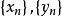
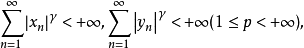
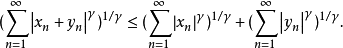
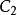
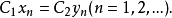
延森不等式
有关凸函式的一个不等式。它的离散形式是
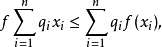
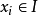
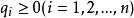
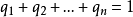
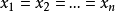
延森不等式的积分形式是
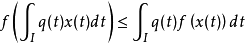
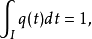
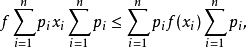
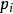
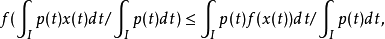
以上不等式中,I可以换成凸集(这时积分应为勒贝格积分)。当f是凹函式时不等号反向。适当地选择f,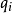 或函式q,可以得到许多着名的不等式。例如,取f(x)=-ln x(x>0)及
或函式q,可以得到许多着名的不等式。例如,取f(x)=-ln x(x>0)及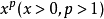 ,可以得到平均不等式与赫尔德不等式。离散形式的延森不等式是赫尔德(Ho¨lder,O.L.)于1889年得到的,积分形式是延森(Jensen,J.L.W.V.)于1906年建立的。
,可以得到平均不等式与赫尔德不等式。离散形式的延森不等式是赫尔德(Ho¨lder,O.L.)于1889年得到的,积分形式是延森(Jensen,J.L.W.V.)于1906年建立的。