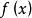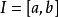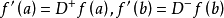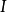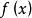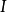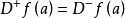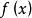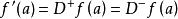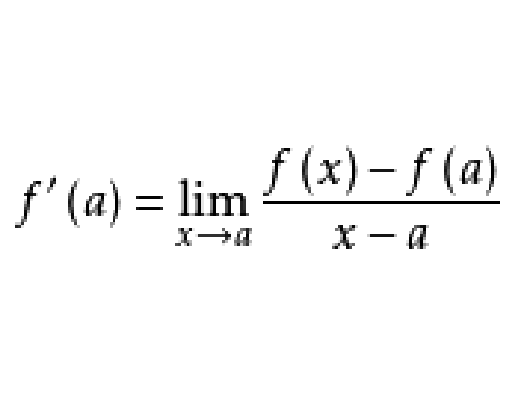微分係数(differential coefficient)即导数,18世纪,拉格朗日(J.-L.Lagrange)在企图用代数方法定义微积分的基本概念时,先定义x的函式的微分A·Δx,再求出它的係数A,并称为微分係数,用通用的语言来说,它就是导数,这个名词今已少用。
基本介绍
- 中文名:微分係数
- 外文名:differential coefficient
- 所属学科:数学(微分学)
- 相关概念:导数,微分,可微等
- 分类:左微分係数,右微分係数
基本介绍
设 是定义在区间
是定义在区间 上的函式,如果a是区间
上的函式,如果a是区间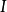 内的一点,那幺
内的一点,那幺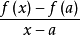 是定义在区间
是定义在区间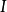 内除a以外的
内除a以外的 点上的函式,此时如果存在极限:
点上的函式,此时如果存在极限:
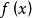
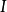
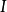
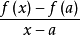
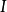

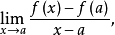
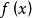
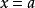
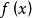
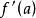
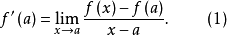
相关概念
可微与导函式
当函式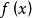 在所属区间内的任意点x均可微时,则称函式
在所属区间内的任意点x均可微时,则称函式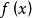 可微,或称函式
可微,或称函式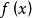 关于 x可微。此时
关于 x可微。此时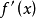 也是定义在区间
也是定义在区间 上的关于x的函式,称
上的关于x的函式,称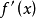 为函式
为函式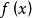 的导函式(derived function derivative),求函式
的导函式(derived function derivative),求函式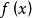 的导函式
的导函式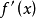 ,称为对函式
,称为对函式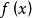 进行微分,或函式
进行微分,或函式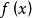 关于x进行微分。
关于x进行微分。
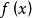
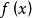
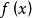
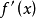
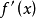
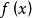
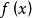
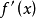
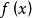
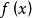
在(1)式中如果用x替换a,用x+h替换x,则
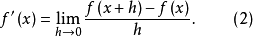
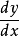
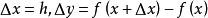
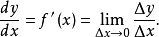
定理1如果函式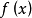 在x点可微,那幺函式
在x点可微,那幺函式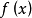 在x点连续。
在x点连续。
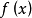
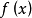
推论定义在某区间上的可微函式在该区间上是连续函式。
无穷小量
当自变数x增加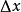 成为
成为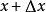 时,相应地函式y也增加
时,相应地函式y也增加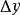 成为
成为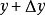 ,因此把
,因此把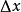 和
和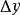 分别称为x和y的增量(increment)。
分别称为x和y的增量(increment)。
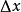
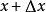
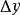
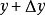
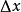
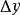
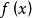
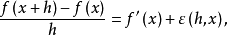
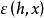
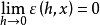
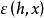

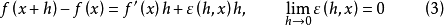
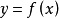
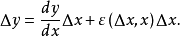
一般地,若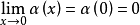 ,则称函式
,则称函式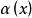 为无穷小量,当
为无穷小量,当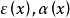 是无穷小量时,无穷小量
是无穷小量时,无穷小量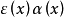 用符号
用符号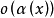 表示,即用小写字母o来代表
表示,即用小写字母o来代表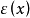 ,在不关心函式
,在不关心函式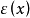 的具体形式时,用符号
的具体形式时,用符号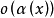 很方便。如果使用这个符号,那幺上式为:
很方便。如果使用这个符号,那幺上式为:
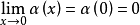
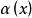
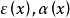
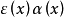
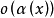
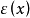
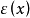
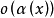
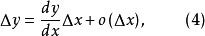
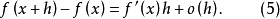
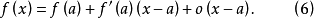
切线
对在a点处可微的函式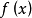 ,把由线性方程式
,把由线性方程式
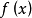
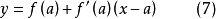
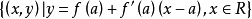
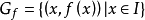
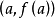
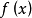
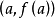
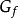
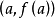
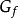
表示函式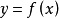 的微分係数的符号除
的微分係数的符号除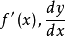 之外,还有
之外,还有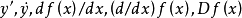 等。
等。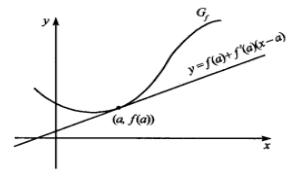 图1
图1
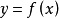
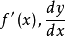
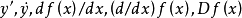
 图1
图1左微分係数和右微分係数
微分係数的定义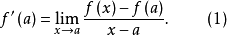 中,当a是
中,当a是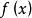 的定义域
的定义域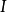 的左端点,例如
的左端点,例如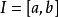 时,
时,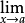 当x从右向a接近时的极限记作
当x从右向a接近时的极限记作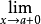 ,所以,
,所以,
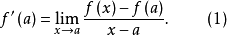
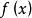
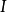
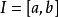
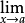
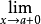
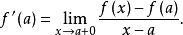
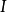
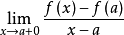
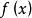
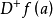
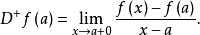
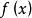
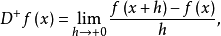
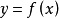
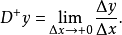
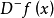
例如,如果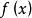 是定义在区间
是定义在区间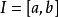 上的可微函式,则
上的可微函式,则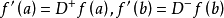 ,又,如果定义在区间
,又,如果定义在区间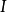 上的函式
上的函式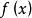 在
在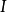 的内点a处左可微和右可微,且
的内点a处左可微和右可微,且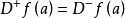 ,那幺
,那幺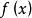 在a点处可微,并且,
在a点处可微,并且,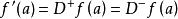 。
。