归一化是一种无量纲处理手段，使物理系统数值的绝对值变成某种相对值关係。简化计算，缩小量值的有效办法。例如，滤波器中各个频率值以截止频率作归一化后，频率都是截止频率的相对值，没有了量纲。阻抗以电源内阻作归一化后，各个阻抗都成了一种相对阻抗值，“欧姆”这个量纲也没有了。等各种运算都结束后，反归一化一切都复原了。信号处理工具箱中经常使用的是nyquist频率，它被定义为採样频率的二分之一，在滤波器的阶数选择和设计中的截止频率均使用nyquist频率进行归一化处理。例如对于一个採样频率为500hz的系统，400hz的归一化频率就为400/500=0.8，归一化频率範围在[0,1]之间。如果将归一化频率转换为角频率，则将归一化频率乘以2*pi，如果将归一化频率转换为hz，则将归一化频率乘以採样频率的一半。

在量子力学里，表达粒子的量子态的波函式必须满足归一条件，也就是说，在空间内找到粒子的机率必须等于1。这性质称为归一性。

一般而言，波函式是一个複函数。可是，机率密度是一个实函式，空间内积分和为1，称为机率密度函式。所以在区域内，找到粒子的机率是1。

因为粒子存在于空间，因此在空间内找到粒子机率是1，所以积分于整个空间将得到1。

假若，从解析薛丁格方程而得到的波函式，其机率是有限的，但不等于1，则可以将波函式乘以一个常数，使机率等于1。或者假若波函式内，已经有一个任意常数，可以设定这任意常数的值，使机率等于1。

1.複数阻抗可以归一化写为：Z = R + jωL = R(1 + jωL/R)（複数部分变成了纯数了，没有任何量纲）。

2.微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

3.在统计学中，归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的机率分布，归一化在-1--+1之间是统计的坐标分布。即该函式在(-∞,+∞)的积分为1。

薛丁格方程为

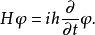
其中，H是表征波函式总能量的哈密顿算符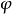，是物理系统的波函式，i是虚数。h是约化普朗克常数。

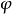
将波函式归一化为。则薛丁格方程成为

对于归一化，薛丁格方程是个不变式，因为薛丁格方程是个线性微分方程。

一个表达粒子量子态的波函式，必须满足粒子的薛丁格方程。既然和都能够满足同样的薛丁格方程，它们必定都表达同样的量子态。假若不使用归一化的波函式，则只能知道机率的相对大小；否则，使用归一化的波函式，可以知道绝对的机率。这对于量子问题的解析，会提供许多便利。

图像中，若比较两张图片（两张图片的样式：通道数，数据格式相同、大小：解析度可以不同）

1.比较两张图片大小，需要判断是否相同的时候；

2.求取较小的一张图片在大图中的位置，需要判断的时候。

这个时候，我们可以使用欧式距离来作为判断函式，如下：

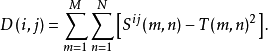
（基础就是二维中的两点的距离： ）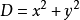

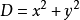
若D=0，说明图片相等；或者是小的一张图片已经找到在大图中的位置。但是上面的D值的取值範围太广，甚至可以达到（0，正无穷大），会超出计算机的计算範围。故使用归一化处理。

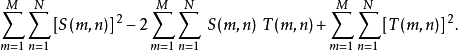
2.可以看出，只有第二项是有意义的，因为第一项和第三项的值在选定模板后是固定的。对于欧式距离相似函式，值越大表示越不相似，也就是说，第二项的值越小则越不相似。

将第二项进行归一化：

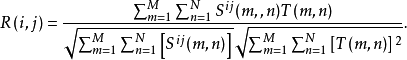
那幺当R（i，j）为1时，表示模板与子图完全相等。