一个距离空间若有可数稠密子集，就称为是可分的。
基本介绍
- 中文名：可分
- 外文名：detachable
- 概述：有可数稠密子集距离空间
- 举例：C[a，b]
- 重要定理：完全有界的距离空间是可分的
- 领域：数学
定义
稠密子集
定义1 设（X，ρ）是一个距离空间，集合E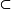
X 满足如下的条件：
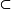
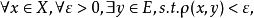
注：易见E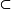X 是X的稠密子集的充分必要条件是：
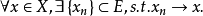例如根据魏尔斯特拉斯定理，[a，b]上的多项式空间P[a，b]在C[a，b]中稠密。
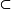
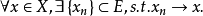
可分性
定义2 一个距离空间若有可数稠密子集，就称为是可分的。
重要结论
定理 完全有界的距离空间是可分的。
证明：取Nn为有穷的1/n网，则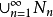
是一个可数稠密子集。
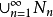
举例
Rn、C[a，b]、Lp[a，b] (1≤p<∞)均是可分的距离空间，L∞[a，b]是不可分的距离空间。