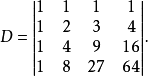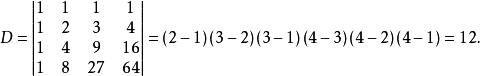一个e阶的范德蒙行列式由e个数c1，c2，…，ce决定，它的第1行全部都是1，也可以认为是c1，c2，…，ce各个数的0次幂，它的第2行就是c1，c2，…，ce（的一次幂），它的第3行是c1，c2，…，ce的二次幂，它的第4行是c1，c2，…，ce的三次幂，…，直到第e行是c1，c2，…，ce的e-1次幂。
基本介绍
- 中文名：范德蒙行列式
- 外文名：Vandermonde determinant
- 所属学科：数学
- 套用：求线形递归方程通解等
定义
形如
定理
若
为
阶范德蒙行列式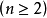
，则有
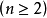
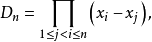
这里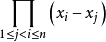
表示所有同类因子
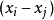(其中
)的乘积，即
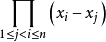
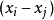
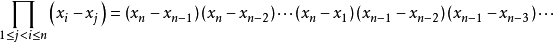
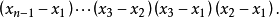
证明 用数学归纳法作证明。
当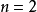
时，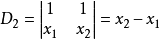
，结论成立，假设该结论对
阶范德蒙行列式成立，即
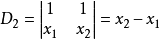
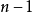
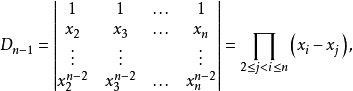
考虑n阶范德蒙行列式的情形
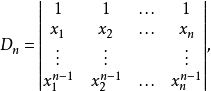
从第n行开始，自上而下依次的由下一行减去它上一行的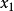
倍 ，有
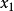
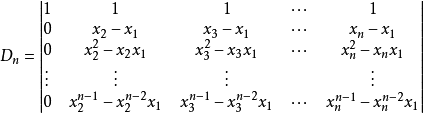
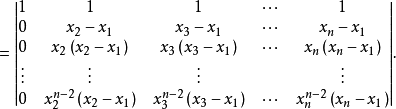
按第一列展开后提取公因式，得
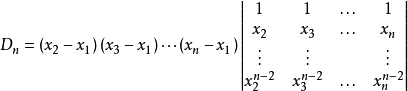
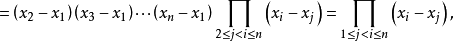
于是有
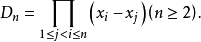
相关计算
例1 计算行列式
