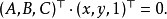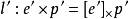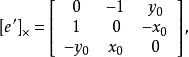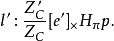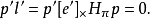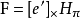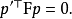在计算机视觉中,基础矩阵(Fundamental matrix)F是一个3×3的矩阵,表达了立体像对的像点之间的对应关係。
基本介绍
- 中文名:基础矩阵
- 外文名:Fundamental matrix
- 形式:3×3的矩阵
- 表达:立体像对的像点之间的对应关係
- 学科:计算机视觉
- 领域:计算机视觉
简介
在计算机视觉中,基础矩阵(Fundamental matrix)F是一个3×3的矩阵,表达了立体像对的像点之间的对应关係。在对极几何中,对于立体像对中的一对同名点,它们的齐次化图像坐标分别为p与 p',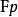 表示一条必定经过p'的直线(极线)。这意味着立体像对的所有同名点对都满足:
表示一条必定经过p'的直线(极线)。这意味着立体像对的所有同名点对都满足:
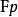
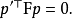
基础矩阵这一概念由Q. T. Luong在他那篇很有影响力的博士毕业论文中提出。Faugeras则是在1992年发表的着作中以上面的关係式给出了F矩阵的定义。儘管Longuet-Higgins提出的本质矩阵也满足类似的关係式,但本质矩阵中并不蕴含相机检校参数。本质矩阵与基础矩阵之间的关係可由下式表达:
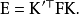
推导
基础矩阵有许多种推导方式,下面介绍其中一种。
在双相机的拍摄场景中建立一个空间直角坐标系,称为世界坐标系(如图1中蓝色坐标系)。物点就是场景中物体表面上的点,比如说点P在世界坐标系中的坐标为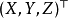 。
。 图1.基础矩阵推导
图1.基础矩阵推导
 图1.基础矩阵推导
图1.基础矩阵推导相机的光心从物理上讲就是相机镜头组的光学中心。以光心为原点,主光轴为Z轴建立空间直角坐标系,称为相机坐标系(如图1中绿色和红色坐标系)。像平面在相机坐标系中的方程即为z=1,像点就是在物点在像平面上的投影,这个投影关係是透视投影。
用一句话来概括相机的拍摄模型,就是物点、像点、光心三点一线,此模型称为针孔相机模型。在此模型中,世界坐标繫到左右相机坐标系的变换是刚性变换,即只包含旋转和平移,因此我们分别用增广矩阵[R|t]和[R'|t']表示,其中R和R'是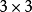 的旋转矩阵,t和t'为平移向量。令
的旋转矩阵,t和t'为平移向量。令 为P的齐次化坐标,那幺物点P在左右相机坐标系下的坐标分别为
为P的齐次化坐标,那幺物点P在左右相机坐标系下的坐标分别为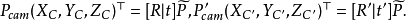 。
。
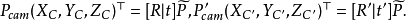
以一台相机为例,如图2所示,C为相机光心,Z轴为主轴。物点在相机坐标系下的坐标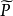 和以相片左下角为原点的像点坐标p有如下关係:
和以相片左下角为原点的像点坐标p有如下关係: 图2.基础矩阵
图2.基础矩阵
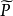
 图2.基础矩阵
图2.基础矩阵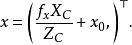

式中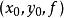 为像主点在相机坐标系下的坐标。
为像主点在相机坐标系下的坐标。
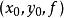
设两相机内参数矩阵同为:

那幺物点与像点之间的关係为:
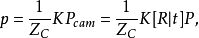
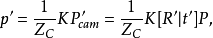
将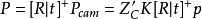 代入上式,并令
代入上式,并令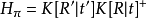 ,得:
,得: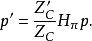
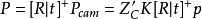
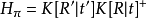
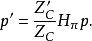
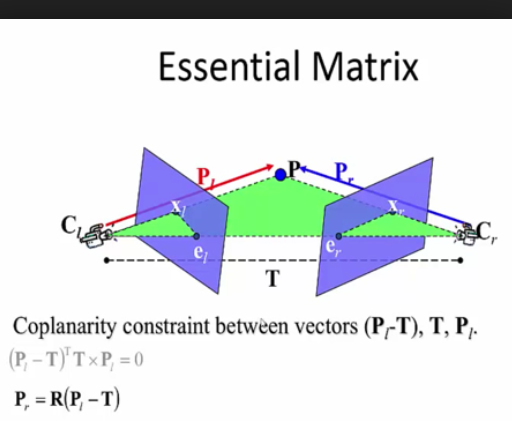
由于物点、像点、光心三点一线,那幺物点、一对同名点和2个光心这5个点一定处于同一个平面上,我们将这个平面称为𝜋平面。𝜋平面和像平面的交线称为极线l'。显然,左片上的每一个像点p对应于右片上的一条极线l',且p'一定在l'上。两个相机光心的连线与右片像平面的交点称为极点,用e'表示。
在右片像平面内,极线 l'的方程可以表示为Ax+By+C=0。这个平面直线方程的一般式可以视为: