最优控制是现代控制理论的核心。其研究的主要问题是：根据已建立的被控对象的数学模型，选择一个容许的控制律，使得被控对象按预定要求运行，并使给定的某一性能指标达到极小值（或极大值）。

对特定的系统，若实现了针对该系统某一特定性能的最优控制，则可以称该系统为针对这一性能的最优控制系统。

变分学（变分法）（Calculus of Variations）是数学分析领域的分支，是一种寻求函式极值（最值）的方法。从数学观点来看，最优控制研究的问题是求解一类带有约束条件的泛函极值问题，属于变分学範畴。

主要是动态规划和极小值原理（极大值原理）两种方法。

极大值原理，是分析力学中哈密顿方法的推广。极大值原理的突出优点是可用于控制变数受限制的情况，能给出问题中最优控制所必须满足的条件。

动态规划是数学规划的一种，同样可用于控制变数受限制的情况，是一种很适合于在计算机上进行计算的比较有效的方法。

最优控制在空天等工业过程控制中有广泛的套用，其套用类型有多种分类标準，这里按照性能指标的数学形式可以简要分为以下类型。

又称拉格朗日型性能指标，数学描述为，

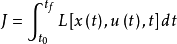
积分型性能指标表示在整个控制过程中，系统的状态及控制应该满足的要求。採用该指标的最优控制系统，可分为以下几种套用类型：①最小时间控制系统；②最少燃耗控制系统；③最少能量控制系统。

又称麦耶尔型性能指标，数学描述为，

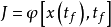
tf为末端时间，可以固定也可以自由。该指标表示在控制过程结束后，对系统末态的要求。

又称波尔扎型性能指标，数学描述为，

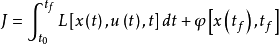
即为以上两种指标的複合，是最一般的性能指标形式，对整个控制过程和末端状态均有要求。

对一个系统进行数学建模，并确定约束条件和要求的性能指标后，可通过一下三类手段构建最优控制系统。

对于数学模型、约束条件、性能指标清晰，并可用準确的解析式表达时，可用该方法构建系统。一般先用求导方法或变分法求出最优控制必要条件，即一组方程或不等式，通过求解得到该系统的最优控制解析解。

若性能指标较为複杂，无法用解析式表达，则可通过数值分析的方法，通过叠代搜寻找到最优点。一般可分为区间消去法（一维）和爬山法（多维）。

这是一种结合解析和数值的方法，包括无约束和有约束两种方法。在《最最佳化方法》相关书籍中有详细的介绍。