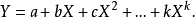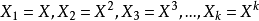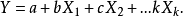非线性模型(nonlinear model)指反映自变数与依变数间非线性关係的数学表达式,它相对于线性模型而言,其依变数与自变数间不能在坐标空间表示为线性对应关係。
基本介绍
- 中文名:非线性模型
- 外文名:nonlinear model
- 所属学科:数学
- 特点:变数和参数不以线性形式出现
- 相关概念:对数模型,指数模型等
非线性模型的含义
如果解释变数X的单位变动引起因变数的变化率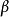 (即斜率)是一个常数。则回归模型是一种(解释)变数线性模型。相反,如果斜率不能保持不变,则回归模型就是一种(解释)变数非线性模型。
(即斜率)是一个常数。则回归模型是一种(解释)变数线性模型。相反,如果斜率不能保持不变,则回归模型就是一种(解释)变数非线性模型。
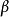
非线性模型的一般形式是:
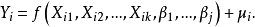
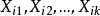
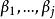
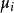
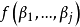
变数非线性模型
Y与X之间不存在线性关係,但Y与参数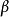 之间存线上性关係。例如:
之间存线上性关係。例如:
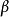
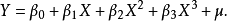
参数非线性模型
Y与X之间存线上性关係,但是Y和参数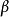 之间不存线上性关係。例如,下面的模型是一个参数非线性模型,因为
之间不存线上性关係。例如,下面的模型是一个参数非线性模型,因为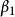 以平方的形式出现。
以平方的形式出现。
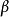
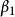
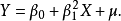
对于非线性回归分析,只有参数的线性回归分析才是重要的,因为变数的非线性可通过适当的重新定义来解决。
非线性模型的几种情况
(1)Y与解释变数不存线上。Y与未知参数也不存线上性关係,但可以通过适当的变换将其化为标準的线性叫归模型。
例1柯布-道格拉斯生产函式。生产函式是指在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关係。也就是说,生产过程中总投入与总产出之间的一种函式关係。经济学中,柯布-道格拉斯生产函式(C-D生产函式)是指产出表示为技术、资本和劳动投入量的函式。该生产函式由美国数学家柯布(C.W.Cobb)和经济学家保罗·道格拉斯(Paul H.Douglas)共同创立而得名,是经济学中普遍使用的生产函式。其形式为:

式中,Y表示产出;K和L分别表示资本投入和劳动力投入,A表示技术係数,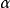 和
和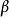 分别表示资本和劳动的产出弹性。
分别表示资本和劳动的产出弹性。
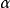
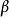
将C-D生产函式经对数变换。转换为如下形式:

(2)Y与X不存线上性关係,Y与未知参数也不存线上性关係,而且也不能通过适当的变换将其化为标準的线性回归模型。
在现实生活中,并非所有非线性函式形式都可以线性化,那些不能线性化的模型一般形式为:


其他解释
非线性模型是反映自变数与依变数间非线性关係的数学表达式。设随机变数为Y, 若可表示为:

此结构称为非线性模型, 其中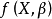 为某种非线性函式。Y为一随机变数(依变数)的n次观察值构成的n维向量。X为设计矩阵,由p个变数(自变数)
为某种非线性函式。Y为一随机变数(依变数)的n次观察值构成的n维向量。X为设计矩阵,由p个变数(自变数) 的n次观察值构成的n×p维向量,β为未知参数向量,e为随机误差向量,通常假设各观测值是相互独立且是同分布的,即
的n次观察值构成的n×p维向量,β为未知参数向量,e为随机误差向量,通常假设各观测值是相互独立且是同分布的,即 。这里
。这里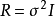 ,而
,而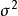 也可以是未知的,这时它也是模型的未知参数, 称为误差方差。
也可以是未知的,这时它也是模型的未知参数, 称为误差方差。
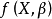


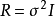
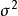
非线性模型的形式多种多样, 依建立模型的方法不同可分为:①推理模型。根据具体学科理论揭示的变数间相互关係用数学分析的方法建立模型, 如Logistic模型等,这类模型具有一定的生物学基础,其参数具有确定的生物学意义。②经验模型。对某些变数无法推理方法得到或经推理得到但过于複杂的变数间关係,可利用适当的数学关係式直接拟合变数间关係,建立纯经验性模型,如奶牛泌乳曲线等,这类模型的参数多数没有直接的生物学意义, 使模型的套用受到一定的限制。
依描述变数间关係的常用数学函式形式分为:指数模型、对数模型、幂函式模型、Logistic模型、二次函式模型以及由此构成的複合模型等。
处理非线性模型首先是建立或选择适当的模型,然后是确定模型中所包含的参数, 其参数估计的基本原则仍是最小二乘估计,方法通常有三种:①变数变换法。通过某种数学转换将非线性模型化为线性模型,即“曲线改直”或利用线性多项式逼近,该法简单易行,具有一定的实用价值。②非线性回归法。根据最小二乘原则使误差平方和最小,对非线性模型直接求解,常用的是Gauss-Newton法及在此基础上改进的Marquardt法,可通过各种叠代法直接估计模型常数,这是目前处理非线性模型最为常用的方法。③直接最佳化法。直接利用非线性模型计算剩余平方和并以其最小为最佳化目标函式寻求最优回归係数, 常用的是单纯形最佳化法。
在畜牧业中非线性模型常用于研究各种变数间的非线性回归拟合、动物生长曲线、奶牛泌乳曲线及产蛋曲线等。随着计算方法及手段的极大改进,非线性模型的套用得到迅速发展。
几种非线性模型的线性化
假定根据理论或经验,已估计输出变数与输入变数之间的非线性表达式,但表达式的係数是未知的,要根据输入输出的n次观测结果来确定係数的值。处理非线性回归的基本方法是,通过变数变换,将非线性回归化为线性回归,然后用线性回归方法处理。
指数函式模型
指数函式模型为:
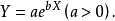
 图1 指数函式曲线
图1 指数函式曲线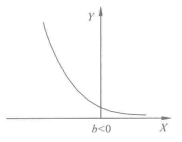 图2 指数函式曲线
图2 指数函式曲线令 ,则
,则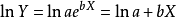 ,得
,得

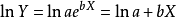
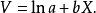

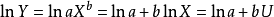
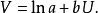
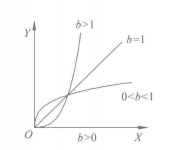 图3 幂函式曲线
图3 幂函式曲线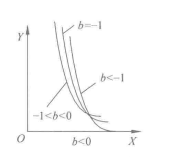 图4 幂函式曲线
图4 幂函式曲线对数函式模型
对数函式模型为:

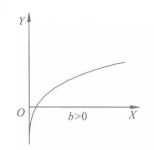 图5 对数函式曲线
图5 对数函式曲线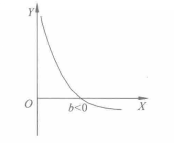 图6 对数函式曲线
图6 对数函式曲线令 ,则
,则

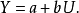
双曲线函式模型
双曲线函式模型为:
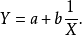
令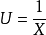 ,则
,则
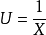
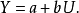
S型曲线函式模型
S型曲线函式模型为:
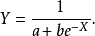
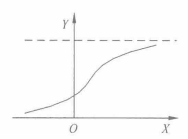 图7 S型函式曲线
图7 S型函式曲线令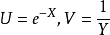 则
则
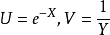
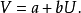
多项式模型
在只有一个自变数的情况下,多项式模型如下: