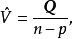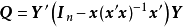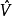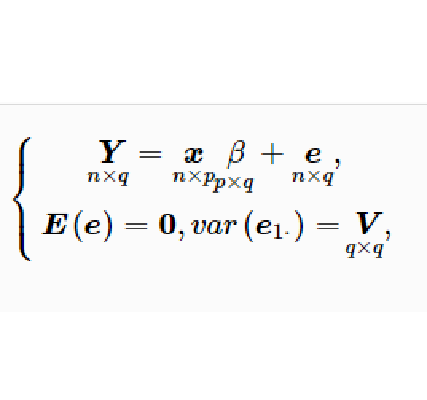多元线性模型(multiple linear model)是数理统计的一个重要分支，在一元线性模型中研究的指标Y是一元随机变数，影响指标Y的因素可以有多个因素，这些因素中可以有定性因子，也可以有定量因子，如果我们研究的指标Y是P元随机变数，影响指标y的因素有多个因素，这就是多元模型的问题。
基本介绍
- 中文名：多元线性模型
- 外文名：multiple linear model
- 所属学科：数学
- 所属领域：数理统计
- 相关概念：一元线性模型、随机变数等
基本介绍
在一元线性模型中，我们研究的指标Y是一元随机变数，影响这个指标的因素却可以有多个，如果我们研究的指标Y是q元随机向量，影响这个指标向量的因素却有p个，并且指标的条件数学期望与这些因素之间满足线性关係，这时就可以用下面将要介绍的多元线性模型来描述指标向量Y和这些因素之间的关係。
假设对应于因素
的指标向量Y的观测值为
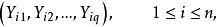
记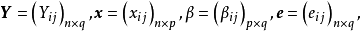
则可以把上面的式子简写为
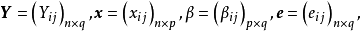
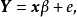
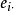
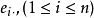
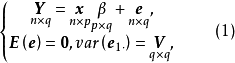
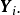
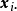
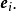
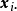
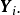
为了方便，我们称n×(q+p)矩阵(Y，x)为资料矩阵；称Y为观测矩阵；称x为设计矩阵：称e为观测误差或模型误差：称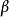
为模型参数矩阵，简称为参数矩阵或参数：称V为方差矩阵，在多元线性模型(1)中，模型的参数矩阵和方差矩阵V是需要估计的参数矩阵、人们最感兴趣的是模型的参数估计问题和有关参数矩阵
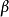的一些假设检验问题。
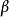
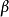
多元线性模型的参数估计
以下只研究多元正态线性模型。
β的最小二乘估计
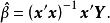
类似于一元线性模型中σ2的估计，我们可以用下面的统计量作为多元线性模型中方差矩阵V的估计：
