DDA算法，是计算机图形学中一种基于直线的微分方程来生成直线的方法，由于有浮点数运算与取整，该算法不利于硬体实现。
基本介绍
- 中文名：DDA算法
- 外文名：DDA algorithm
- 全称：Digital Differential Analyzer
- 别名：数值微分法
算法思想
直线的基本微分方程为：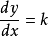
。
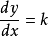
设直线通过点
和
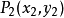，则直线方程可表示为：
。
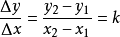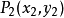
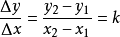
如果已知第
点的坐标，可用步长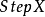
和
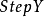得到第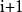
点的坐标为：
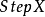
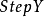
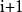
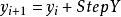
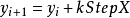
如下图：
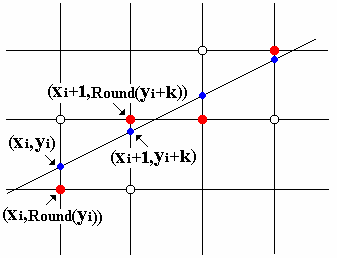
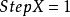
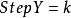
将算得的直线上每个点的当前坐标，按四捨五入得到光栅点的位置。
算法描述
DDA算法的C语言描述如下。当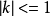
时，实现代码：
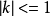
voidDDALine(intx0,inty0,intx1,inty1,intcolor){intx;floatdx,dy,y,k;dx=x1-x0,dy=y1-y0;k=dy/dx,y=y0;for(x=x0;x<=x1;x++){Drawpixel(x,int(y+0.5),color);y=y+k;}}当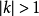
时，实现代码：
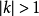
voidDDALine(intx0,inty0,intx1,inty1,intcolor){inty;floatdx,dy,x,k;dx=x1-x0,dy=y1-y0;k=dx/dy,x=x0;for(y=y0;y<=y1;y++){Drawpixel(int(x+0.5),y,color);x=x+k;}}任意斜率代码实现如下：（注意自己补上，此处n做分母可能为0）
voidDDALine(intx0,inty0,intx1,inty1,intcolor){ intdx,dy,n,k;floatxinc,yinc,x,y;dx=x1-x0;dy=y1-y0;if(abs(dx)>abs(dy))n=abs(dx);elsen=abs(dy);xinc=(float)dx/n;yinc=(float)dy/n;x=(float)x0;y=(float)y0;for(k=1;k<=n;k++){Drawpixel(int(x+0.5),int(y+0.5),color);x+=xinc;y+=yinc;}}