字元串和编码的对应关係是在压缩过程中动态生成的，并且隐含在压缩数据中，解压的时候根据表来进行恢复，算是一种无损压缩.

根据 Lempel-Ziv-Welch Encoding ，简称 LZW 的压缩算法，用任何一种语言来实现它.

LZW压缩算法的基本概念：LZW压缩有三个重要的对象：数据流（CharStream）、编码流（CodeStream）和编译表（String Table）。在编码时，数据流是输入对象（文本档案的据序列），编码流就是输出对象（经过压缩运算的编码数据）；在解码时，编码流则是输入对象，数据流是输出对象；而编译表是在编码和解码时都须要用藉助的对象。

字元（Character）：最基础的数据元素，在文本档案中就是一个位元组，在光栅数据中就是一个像素的颜色在指定的颜色列表中的索引值；

字元串（String）：由几个连续的字元组成；

前缀（Prefix）：也是一个字元串，不过通常用在另一个字元的前面，而且它的长度可以为0；

根（Root）：一个长度的字元串；

编码（Code）：一个数字，按照固定长度（编码长度）从编码流中取出，编译表的映射值；图案：一个字元串，按不定长度从数据流中读出，映射到编译表条目.

LZW压缩算法的基本原理：提取原始文本档案数据中的不同字元，基于这些字元创建一个编译表，然后用编译表中的字元的索引来替代原始文本档案数据中的相应字元，减少原始数据大小。看起来和调色板图象的实现原理差不多，但是应该注意到的是，我们这里的编译表不是事先创建好的，而是根据原始档案数据动态创建的，解码时还要从已编码的数据中还原出原来的编译表.

LZW算法基于转换串表（字典）T，将输入字元串映射成定长（通常为12位）的码字。在12位4096种可能的代码中，256个代表单字元，剩下3840给出现的字元串。

LZW算法流程图

LZW字典中的字元串具有前缀性，即 ωK∈T=>；ω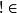T。

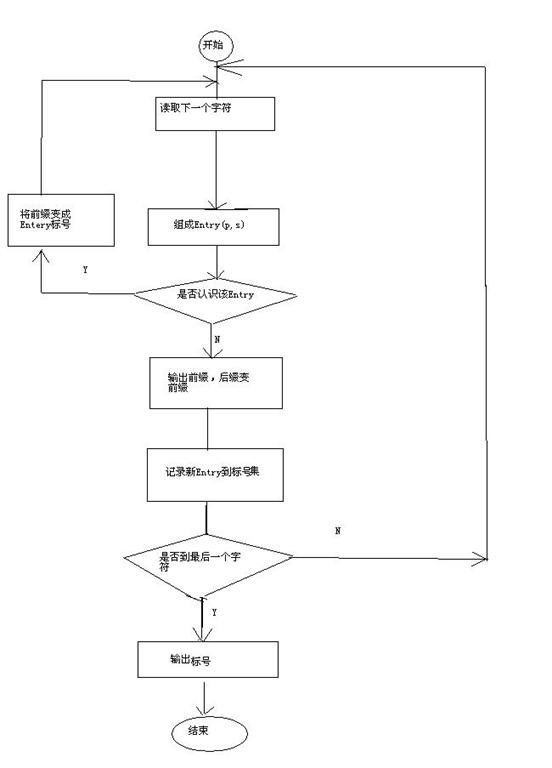
LZW算法流程：

具体解压步骤如下：

(1)解码开始时Dictionary包含所有的根。

(2)读入在编码数据流中的第一个码字 cW(它表示一个Root)。

(3)输出String.cW到字元数据流Charstream。

(4)使pW=cW 。

(5)读入编码数 据流 的下一个码字cW 。

(6)目前在字典中有String.cW吗?

YES：1)将String．cW输出给字元数据流；

2)使P=String.pW；

3)使C=String.cW的第一个字元；

4)将字元 串P+C添 加进Dictionray。

NO ：1)使P=String.pW ；

2)使C=String.pW的第一个字元；

3)将字元串P+C输出到字元数据流并将其添加进Dictionray(现在它与cW相一致)。

(7)在编码数据 流中还有Codeword吗?

YES：返回(4)继 续进行 解码 。

NO：结束解码 。

LZW码能有效利用字元出现频率冗余度进行压缩，且字典是自适应生成的，但通常不能有效地利用位置冗余度。

具体特点如下：

l)LZW压缩技术对于可预测性不大的数据具有较好的处理效果，常用于TIF格式的图像压缩，其平均压缩比在2：1以上，最高压缩比可达到3：1。

2）对于数据流中连续重複出现的位元组和字串，LZW压缩技术具有很高的压缩比。

3）除了用于图像数据处理以外，LZW压缩技术还被用于文本程式等数据压缩领域。

4)LZW压缩技术有很多变体，例如常见的ARC、RKARC、PKZIP高效压缩程式。

5）对于任意宽度和像素位长度的图像，都具有稳定的压缩过程。压缩和解压缩速度较快。

6）对机器硬体条件要求不高，在 Intel 80386的计算机上即可进行压缩和解压缩。