格兹尔算法( Goertzel algorithm )是数位讯号处理的一种运算技巧,此运算技巧提供一个有效率的方式来估计部分区域的离散傅立叶转换,广泛的运用在数字电话中的的双音多频信号(每个拨号的数字键由两个频率的音所组成,一个低频,一个高频),此算法在1958年被杰拉德·格策尔( Gerald Goertzel )所提出。
基本介绍
- 中文名:格兹尔算法
- 外文名:Goertzel algorithm
- 领域:数位讯号处理
- 用途:估计部分区域的离散傅立叶转换
- 提出者:杰拉德·格策尔
- 时间:1958
简介
格策尔算法把离散傅立叶转换看成是一组滤波器,将输入的讯号与滤波器中的脉冲回响做卷积运算,求的滤波器的输出。格策尔算法与离散傅立叶转换的相似处在于他们都可以分析某个特定频段的离散讯号;相反的,它们的不同处在于,格策尔算法每次叠代的运算都是使用实数的乘法。虽然说在全频域的计算上,格策尔算法会比其他的傅立叶转换快速算法的複杂度来的高,但是它能区段式的分析每个小区段的频率组成,因此可以编写成较简单的运算架构,实际套用在处理器内的数值计算会更有效率。格策尔算法逆向操作生成出弦波,而这个过程只需花费一个乘法和一个加法运算。
算法
格策尔算法利用旋转因子 的周期性,将离散傅立叶转换转换为线性的滤波运算。旋转因子原来是指在Cooley-Tukey快速傅立叶变换算法的蝴蝶形运算中所乘上的複数常数,因此常数在複数平面上位于单位圆之上,对于被乘数在複数平面上面会有旋转的效果,故名为旋转因子,后来也会用来指称FFT中的任一常数乘法。因为旋转因子:
的周期性,将离散傅立叶转换转换为线性的滤波运算。旋转因子原来是指在Cooley-Tukey快速傅立叶变换算法的蝴蝶形运算中所乘上的複数常数,因此常数在複数平面上位于单位圆之上,对于被乘数在複数平面上面会有旋转的效果,故名为旋转因子,后来也会用来指称FFT中的任一常数乘法。因为旋转因子:

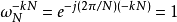
可得转换后第k点的频率为

定义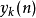 为
为
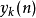
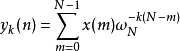
可将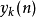 理解为由两个讯号的卷积运算得出的结果
理解为由两个讯号的卷积运算得出的结果
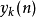

其中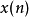 式输入的N点讯号,另外一个
式输入的N点讯号,另外一个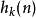 则被看作是IIR滤波器的脉冲频率回响
则被看作是IIR滤波器的脉冲频率回响
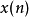
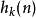
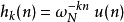
当n=N时,滤波器的输出 即为
即为


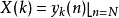
对公式中Z进行转换,可得一阶IIR转移函式
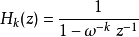
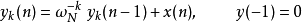
依照此差分方程进行叠代运算,叠代到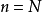 时即可依据上述公式得到
时即可依据上述公式得到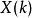 。而依照转移函进行运算时,可以先将旋转因子
。而依照转移函进行运算时,可以先将旋转因子 储存起来,每次叠代包含一次複数乘法,则按照公式计算N点离散傅立叶转换时则需要
储存起来,每次叠代包含一次複数乘法,则按照公式计算N点离散傅立叶转换时则需要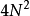 次实数乘法运算和
次实数乘法运算和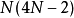 次加/减法,加/减法与乘法运算皆为
次加/减法,加/减法与乘法运算皆为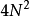 次,当N不大时运算效率不佳,若改为接下来改进的的格策尔算法(二阶),所需的实数乘法次数约为原本的一半。
次,当N不大时运算效率不佳,若改为接下来改进的的格策尔算法(二阶),所需的实数乘法次数约为原本的一半。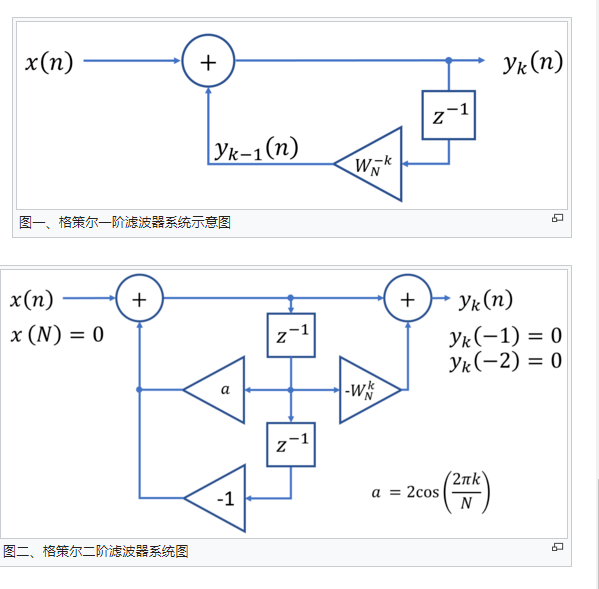 算法流程图
算法流程图
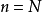
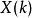

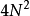
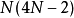
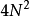
 算法流程图
算法流程图上下同乘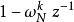 ,可得第k点的频率回响转移函式为
,可得第k点的频率回响转移函式为
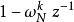
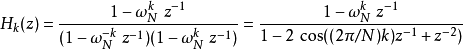
可得知此二阶滤波器有一对共轭的极点与一个零点。在计算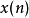 的转换结果
的转换结果 时,会有两个步骤:
时,会有两个步骤:
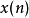

共轭极点叠代计算 依序将输入讯号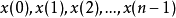 放入滤波器做叠代运算,共作N次叠代,计算量是
放入滤波器做叠代运算,共作N次叠代,计算量是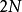 次实数乘法与
次实数乘法与 次实数加/减法
次实数加/减法
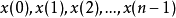
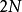

零点叠代计算 输入讯号 是N点的讯号从
是N点的讯号从 。加入
。加入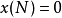 的边界条件,可以按照流程图计算出
的边界条件,可以按照流程图计算出 ,此即为所求的
,此即为所求的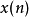 离散傅立叶转换
离散傅立叶转换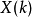 ,此步骤的计算量为4次实数乘法与4次实数加/减法。综合以上步骤,总共的计算量为
,此步骤的计算量为4次实数乘法与4次实数加/减法。综合以上步骤,总共的计算量为 次实数乘法运算以及
次实数乘法运算以及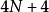 次实数加法运算,而使用此计算算法只需储存
次实数加法运算,而使用此计算算法只需储存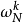 与
与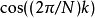 两个参数。
两个参数。


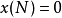

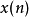
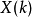

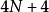
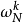
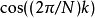
离散傅立叶变换
傅立叶变换(Fourier transform)是一种线性积分变换,用于信号在时域(或空域)和频域之间的变换。离散傅立叶变换(Discrete Fourier Transform,缩写为DFT),是傅立叶变换在时域和频域上都呈离散的形式,将信号的时域採样变换为其DTFT的频域採样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作其周期延拓的变换。在实际套用中通常採用快速傅立叶变换计算DFT。

