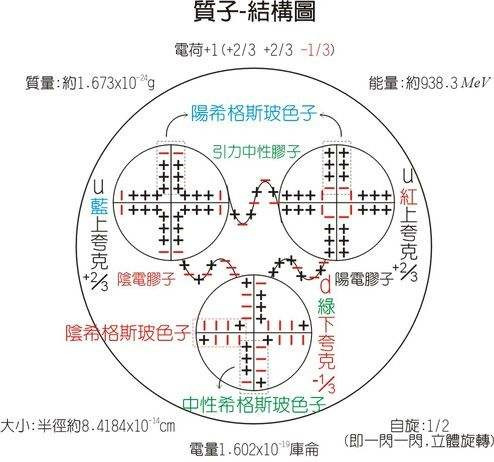
量子色动力学(Quantum Chromodynamics,简称QCD)是在阿德勒、伯约肯以及其他人工作的基础上,在1972年由盖尔曼和弗里奇所创立。它是一种强相互作用的规範理论,它描述组成强作用粒子(强子)的夸克和与色量子数相联繫的规範场的相互作用,可以统一地描述强子的结构和它们之间的强相互作用,被认为是有希望的强作用基本理论。
基本介绍
- 中文名:量子色动力学
- 外文名:Quantum Chromodynamics
- 作用:描述夸克之间强相互作用
- 套用领域:量子力学
- 创立时间:1972年
- 创立者:盖尔曼和弗里奇
强子结构
按照夸克模型,所有重子都由三个夸克组成,所有介子都由一对正反夸克组成。夸克的自旋为1/2。为组成实验观察到的重子和介子,须认为夸克有许多种,在文献上称为夸克的味。为使重子内部波函式有费密统计所要求的全反对称性,并说明重子由三个夸克组成,人们提出夸克还具有另一种内部自由度,它可以取三种不同的状态,人们借用光学中的辞彙称它们有三种不同的色。
重子中的三个夸克各带不同的色。介子中的正反夸克对带相反的色量子数。重子和介子都不带色量子数,它们是“白色”的。三种色夸克在强作用中的性质完全相似,因此强作用有与此相应的对称性。以ψia代表夸克场,其中i=1,2,3代表三种色,a=1,2,3……代表不同的味,则理论在幺正变换下保持形式不变,这里U=(Uij)构成三行三列的幺正矩阵。
色规範场
假设上述强作用的 SU(3)对称性是定域的对称性,即当群参量Θα是时空坐标t和x的函式时,理论仍保持不变,就引导到色规範场的概念。在这个规範理论中,除夸克场ψia外还有八个规範场Aα(α=1,2,...…,8),分别与八个守恆流耦合。
如果假设上述强作用的 SU(3)对称性是定域的对称性,即当群参量Θα是时空坐标t和x的函式时,理论仍保持不变,就引导到色规範场的概念。在这个规範理论中,除夸克场ψia外还有八个规範场Aα(α=1,2,...…,8),分别与八个守恆流耦合。SU(3)定域规範不变的要求唯一地确定拉氏函式密度的形式

式中
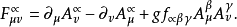
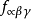
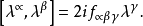
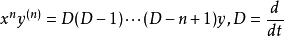


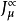
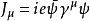
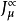
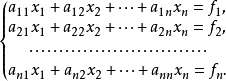
规範理论
微扰量子色动力学与渐近自由。量子色动力学属于规範理论,因而是可重正化的。它的微扰论展开式可以计算到高阶。在其他的强作用量子场论中,由于耦合常数大,微扰论展开式不能用来作可靠的计算。在这方面量子色动力学有它独特之处。在量子电动力学中,由于真空极化的禁止作用,使电子的有效电荷随着对电子距离减小而变大。 重正化
重正化
 重正化
重正化性质
非交换群规範场理论以外的其他可重正化场论几乎都有类似的性质,它们的有效耦合常数随距离减小而增加,即在小距离内作用变强。非交换群规範理论则不同。研究表明,规範场的自作用能够产生相反的效果,使得放在真空中的色荷吸引真空中产生的规範粒子,在它的周围聚集相同的色荷,造成反禁止的效应。
种类
在夸克的味不超过16种时,真空中胶子分布所产生的反禁止效应超过夸克对产生的禁止效应。在这种情况下量子色动力学有所谓渐近自由的性质,即随着时空距离的变小相互作用变弱,有效耦合常数随距离趋于零。按照测不準关係,小的时空距离相应于大的能量动量。某些高能过程的物理量主要与小的时空距离有关。对于这些物理量,量子色动力学中按有效耦合常数的幂次的微扰论展开式,在高能下很快地收敛,因此可以作可靠的计算。迄今为止,别的强作用理论都由于没有小参量而无法作可靠的近似,量子色动力学在这方面是唯一的例外。
无关性
强作用的近似标度无关性 70年代中, 在轻子的深度非弹性散射的单举截面、正负电子对撞产生强子的总截面及这些过程中产生的强子喷注等一系列高能实验中,发现强作用有一些未曾预料到的性质。所谓轻子的非弹性散射是指电子e与核子N碰撞而产生一些强子,e+N→e+N+强子,或中微子v与核子N碰撞转化成μ子和一些强子,v+N→μ+强子。这两个过程分别是电磁作用和弱作用过程,同时也有强作用参加。如果在碰撞中轻子动量传递的二次方q2和能量损失(mN 是核子的质量)都很大,则这个过程称为深度非弹性散射。在单举截面中,只测量轻子。 质心繫总能量W
质心繫总能量W
 质心繫总能量W
质心繫总能量W动量
因此这个截面只是 q2和 v 的函式。单举截面决定于几个称为结构函式的无量纲的量。这些结构函式只与强作用有关。实验发现在 q2和v都很大时它们近似地只依赖于比值x=q2/2v,对固定的x,它们随q2的变化很缓慢。正负电子对撞产生强子和产生 μ子对的总截面的比 r是正负电子对的质心系总能量W 的函式。实验发现,在W大时R近似地是常数(除在某些产生新粒子的阈能附近以外)。这些及其他一些实验结果可以解释为强作用中没有一个在高能下起作用的固有的能量标度,在有关的能量、动量都很高时,粒子的质量及其他有质量或能量量纲的常数都可以忽略,因此只依赖于强作用的无量纲的量都只是有关的能量、动量的比的函式,而不是某个能量、动量与某个有量纲常数的比的函式。这就是实验所揭示的强作用在高能下的近似。
标度无关性
然而在可重正化场论微扰展开式的高阶中总是要出现形式的因子,这里g是耦合常数,E是某个能量,μ是粒子质量或由重正化引进的参量。这样的项在E2很大时并不能忽略。因此至少在微扰论範围内一般的可重正场论没有无标度性。但是对量子色动力学这样的渐近自由的理论,有效耦合常数在有关的能量、动量趋于无穷大时趋于零。因此,在上述高能过程中标度无关性在极限下可以保持或只有轻微的破坏。这种定性的成功使得量子色动力学受到人们的重视。量子色动力学的微扰论计算结果与轻子深度非弹性散射、电子正电子碰撞产生强子、喷注现象等高能过程的实验数据是一致的。理论与实验在各种过程中的定量比较还需要继续进行。
强子结构
在量子色动力学中夸克的质量不大,胶子的质量为零,它们应当很容易产生。因此必须解释为什幺没有在实验中观察到这些粒子。作为强作用的基本理论,人们还需要量子色动力学来得到强子谱和强子的结构,这些问题不能在微扰论的範围内得到解答。人们构想夸克和胶子这样的带色量子数的粒子是由于规範场相互作用的动力学的原因而被禁闭在强子半径10-13cm的範围内。只有强子这样的白色的複合粒子才能作为自由粒子而出现。这种色量子数的禁闭或者是绝对的或则是近似的。人们从不同的角度给出论据,企图说明色的禁闭在量子色动力学中是成立的。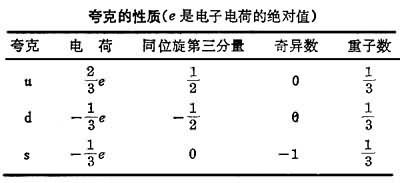 强子结构
强子结构
 强子结构
强子结构论据
一些论据给出如下的图像。与电磁场的电力线相似,色规範场也可以用力线描述。两个相反的色荷之间有力线相连线。在量子色动力学中的力线不像两个相反电荷之间的电力线那样分散在空间而是集中在两个色荷的连线上形成一根弦。人们把这种情况与穿入第二类超导体中的磁力线相比,这时磁力线受超导体的排斥而形成细管。规範场力线的弦中带有正比于弦的长度的能量,当两个色荷之间的距离增加趋于无穷时,弦所带的能量也将趋于无穷。在此以前弦可以断裂而产生一对新的相反的电荷。每段弦的两端都有一对相反的色荷。无论是哪种情况,都不能把两个色荷分开到大的距离。因此这个图像给出色禁闭。对这个图像的一个支持来自格点规範理论。在格点规範理论中连续的时空被离散的格点所代替。规範场和与它作用的费密场分别定义在联接相邻格点的线和格点本身所组成的点阵上。拉氏函式满足离散格点上的规範不变性。当两个格点间的距离a趋于零时,格点规範理论趋于连续时空的规範理论。与连续时空规範理论的渐近自由相对应,在格点规範理论中,如果固定某个物理量的数值则耦合常数g随格点间的距离 a减小而减小。在a趋于零时格点规範理论可以用弱耦合展开,它趋于连续理论的微扰论。
微扰论
在a大时g的值大,应当用强耦合展开,即展开成的幂级数。在强耦合极限下证明了非交换群格点规範理论中两个色荷之间的力线聚集成弦,因而有色禁闭。为证明连续理论有色禁闭还需要证明在耦合由强变弱时色禁闭的性质不消失。在电子计算机上用蒙特-卡罗法。对格点数不多的点阵进行研究的结果表明,对于一段中间的g值计算结果可以同时与色禁闭的弦和连续理论的渐近自由微扰展开式一致。这个结果支持连续时空的规範理论有色禁闭的性质。格点规範理论的研究没有发现在 g变小的过程中存在解除色禁闭的“相变”。虽然如此,连续时空规範理论的色禁闭还只是一种有某些根据的猜测,这是量子色动力学中还存在的一个基本问题。至于强子谱的研究更是处于开始的阶段。