磁矢势，又称磁位、磁势（magnetic potential），通常标记为。磁矢势的旋度是磁场的磁感应强度(矢量)，以方程表示

其中，是磁场的磁感应强度(矢量)。

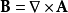
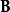
直观而言，磁矢势似乎不及磁场来得“自然”、“基本”，而在一般电磁学教科书亦多以磁场来定义磁矢势。以前，很多学者认为磁矢势并没有实际意义，只是人为的物理量，除了方便计算以外，别无其它用途。但是，詹姆斯·麦克斯韦颇不以为然，他认为磁矢势可以诠释为“每单位电荷储存的能量”，就好像电势被诠释为“每单位电荷储存的能量”。相关论述，稍后会有更详尽解释。

磁矢势并不是唯一定义的；其数值是相对的，相对于某设定数值。因此，学者会疑问到底储存了多少动量？不论如何，磁矢势确实具有实际意义。尤其是在量子力学里，于1959年，阿哈诺夫－波姆效应阐明，假设一个带电粒子移动经过某零电场、零磁场、非零磁矢势场区域，则此带电粒子的波函式相位会有所改变，因而导致可观测到的干涉现象。现在，越来越多学者认为电势和磁矢势比电场和磁场更基本。不单如此，有学者认为，甚至在经典电磁学里，磁矢势也具有明确的意义和直接的测量值。

磁矢势与电势可以共同用来设定电场与磁场。许多电磁学的方程可以以电场与磁场写出，或者以磁矢势与电势写出。较高深的理论，像量子力学理论，偏好使用的是磁矢势与电势，而不是电场与磁场。因为，在这些学术领域里所使用的拉格朗日量或哈密顿量，都是以磁矢势与电势表达，而不是以电场与磁场表达。

开尔文男爵最先于1851年引入磁矢势的概念，并且给定磁矢势与磁场之间的关係。

主条目：电磁四维势

在解析狭义相对论问题时，很自然而然地会将磁矢势与电势连结在一起，成为电磁四维势。这样做法主要基于三个动机：

电磁四维势定义为

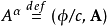
洛伦茨规範以抽象指标记号表示为

其中

是对于反变矢量的偏微分。

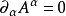
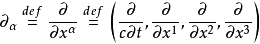
麦克斯韦方程组写为

其中， 是四维电流密度。

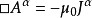
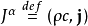
前面谈到电势和磁矢势分别诠释为每单位电荷储存能量和每单位电荷储存动量。这可以从它们的四维矢量观察出来。思考四维动量，它是由能量{\displaystyle E}与动量{\displaystyle \mathbf {p} }共同组成的四维矢量：

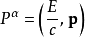
改变观测的参考系，四维动量的四个分量会有对应的改变，电磁四维势也会有类似的改变。假若，电磁四维势的电势可以诠释为每单位电荷储存能量，那幺，电磁四维势的磁矢势应该也有足够的理由诠释为每单位电荷储存动量。

麦可·法拉第最先提出电紧张态的概念。在研究电磁感应理论时，他发现当将物体放在磁铁或电流的附近时，物体会进入一种状态。假若不打扰这系统，则处于此状态的物体不会自发地显示出任何现象。但是，一当系统有所变化，像磁铁被移动了，或电流被增大了，则这状态也会改变，因而产生电流或趋向产生电流。法拉第称此状态为“电紧张态”。但是，这概念并没有被很明确地说明。

后来，开尔文男爵于1851年引入磁矢势的概念，并且给定磁矢势与磁场之间的关係：

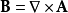
在论文《论法拉第力线》的后半部分，麦克斯韦开始仔细分析电紧张态的物理性质。他给出一条重要定律：作用于一个导体的微小元素的电场，可以由该微小元素的电紧张态对于时间的导数来衡量。以现代标记表示，这方程为

这是麦克斯韦学术生涯中的第一个重要突破，他将

法拉第的电紧张态辨识为开尔文男爵的磁矢势，并且对于电紧张态给出严格定义。

对于电紧张态的定义式取旋度，则可得到法拉第感应方程：

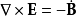
麦克斯韦在他的论文里特别提出，开尔文男爵于1851年发现的关于磁矢势的数学性质，即任意添加一个函式的梯度给磁矢势，都不会改变磁矢势与磁场的关係式、法拉第感应方程，这数学性质后来演化为现今规範自由的概念。