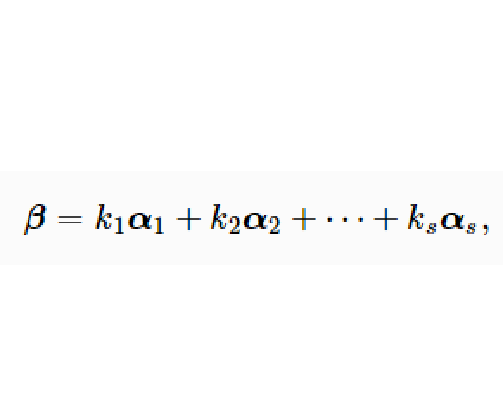线性组合是线性代数的基本概念之一,设α1,α2,…,αe(e≥1)是域P上线性空间V中的有限个向量,若V中向量α可以表示为α=k1α1+k2α2+…+keαe(ka∈P,a=1,2,…,e),则称α是向量组α1,α2,…,αe的一个线性组合,亦称α可由向量组α1,α2,…,αe线性表示或线性表出。
基本介绍
- 中文名:线性表出
- 外文名:linear expression
- 所属学科:数理科学
- 相关概念:线性组合、线性表示等
定义
若干个同维数的行向量(或同维数的列向量)所组成的集合叫做向量组。
对n维向量 和
和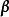 ,如果存在实数
,如果存在实数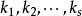 ,使得
,使得

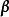
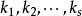
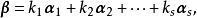
称向量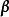 是向量
是向量 的线性组合,或者说向量
的线性组合,或者说向量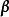 可由
可由 线性表出(示)。
线性表出(示)。
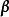

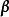

设有两个n维向量组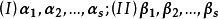 ;如果
;如果 中每个向量
中每个向量 都可由
都可由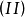 中的向量
中的向量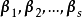 线性表出,则称向量组
线性表出,则称向量组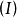 可由向量组
可由向量组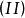 线性表出。
线性表出。
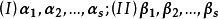


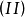
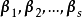
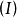
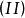
如果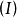 、
、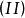 这两个向量组可以互相线性表出,则称这两个向量组等价。
这两个向量组可以互相线性表出,则称这两个向量组等价。
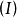
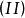
注:(1)等价向量组具有传逆性、对称性、反身性;
(2)向量组和它的极大线性无关组是等价向量组;
(3)向量组的任意两个极大线性无关组是等价向量组;
(4)等价的向量组有相同的秩。但秩相等的向量组不一定等价。
例题解析
例1 已知
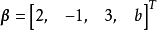 ,试问当a,b取何值时
,试问当a,b取何值时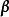 可以由
可以由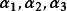 线性表示,并写出其表达式。
线性表示,并写出其表达式。

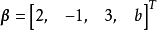
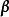
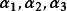
解: 设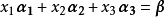 ,按分量写出,即有
,按分量写出,即有
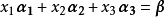
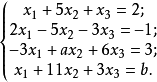
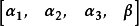
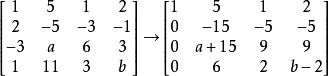

如果b≠4,方程组无解,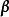 不能由
不能由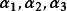 线性表出。
线性表出。
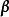
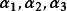
如果b=4,秩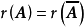 方程组有解,
方程组有解,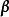 可由
可由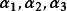 线性表出。
线性表出。
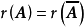
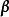
(1)当 时,
时,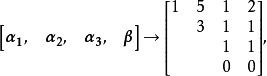

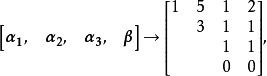
方程组有唯一解: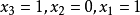 ,即
,即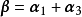 。
。
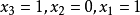
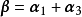
(2)当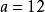 时,
时,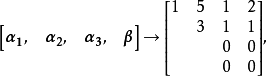
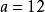
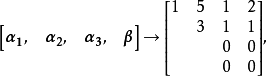
方程组有无穷多解: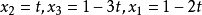 ,即
,即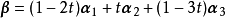 ,t为任意实数。
,t为任意实数。
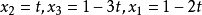
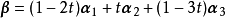
例2 设有向量组(1): ;
;

(2):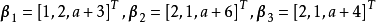 。
。
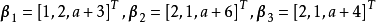
试问:当a为何值时,向量组(1)与(2)等价?当a为何值时,向量组(1)与(2)不等价?
分析: 所谓向量组(1)与(2)等价,即向量组(1)与(2)可以互相线性表出,如果方程组
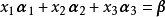
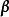
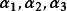
那幺,如果对同一个a,三个方程组



解: 对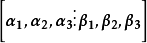 作初等行变换,有
作初等行变换,有
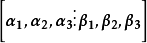


那幺,由方程组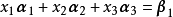 知,只要
知,只要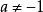 方程组总有唯一解,即
方程组总有唯一解,即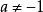 时,
时,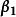 必可由
必可由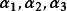 线性表出,而
线性表出,而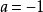 时,方程组无解,
时,方程组无解,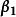 不能由
不能由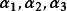 线性表出。
线性表出。
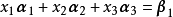
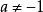
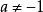
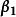
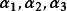
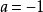
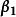
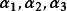
由方程组 知,
知, 方程组总有解,即
方程组总有解,即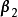 必可由
必可由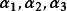 线性表出。
线性表出。


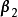
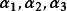
由方程组 知,只要
知,只要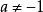 ,方程组就有解,
,方程组就有解,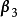 就可由
就可由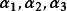 线性表出,
线性表出,

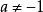
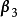
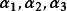
因此,当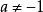 时,向量组(2)可由向量组(1)线性表出。
时,向量组(2)可由向量组(1)线性表出。
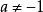
反之,由于行列式
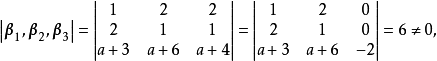
故 ,三个方程组
,三个方程组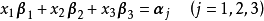 恆有解,即
恆有解,即 ,向量组(1)总可由向量组(2)线性表出,因此,
,向量组(1)总可由向量组(2)线性表出,因此,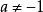 时向量组(1)与(2)等价。
时向量组(1)与(2)等价。

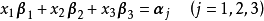

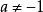
而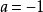 时,
时,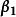 不能由
不能由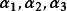 线性表出,向量组(1)与(2)不等价。
线性表出,向量组(1)与(2)不等价。
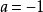
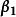
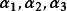
评注: 若未知向量的坐标而要判断能否线性表出的问题,通常是转换为非齐次线性方程组是否有解的讨论,如果向量的坐标没有给出而问能否线性表出,通常用线性相关及秩的理论分析、推理。