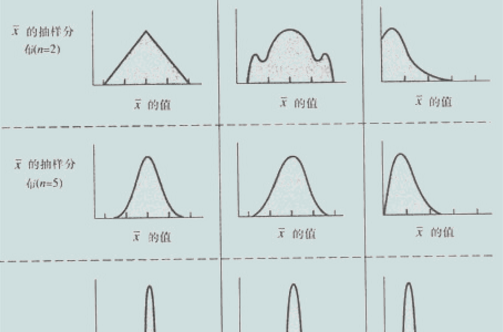
中心极限定理,是指机率论中讨论随机变数序列部分和分布渐近于常态分配的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变数近似服从常态分配的条件。它是机率论中最重要的一类定理,有广泛的实际套用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从常态分配的。中心极限定理就是从数学上证明了这一现象。最早的中心极限定理是讨论重点,伯努利试验中,事件A出现的次数渐近于常态分配的问题。
基本介绍
- 中文名:中心极限定理
- 外文名:central limit theorem
- 提出者:法国数学家棣莫弗
- 套用学科:机率论
- 适用领域範围:自然界与生产中
- 适用领域範围:数理统计学和误差分析
简介及其历史发展
它是机率论中最重要的一类定理,有广泛的实际套用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从常态分配的。中心极限定理就是从数学上证明了这一现象 。最早的中心极限定理是讨论n重伯努利试验中,事件A出现的次数渐近于常态分配的问题。1716年前后,A.棣莫弗对n重伯努利试验中每次试验事件A出现的机率为1/2的情况进行了讨论,随后,P.-S.拉普拉斯和A.M.李亚普诺夫等进行了推广和改进。自P.莱维在1919~1925年系统地建立了特徵函式理论起,中心极限定理的研究得到了很快的发展,先后产生了普遍极限定理和局部极限定理等。极限定理是机率论的重要内容,也是数理统计学的基石之一,其理论成果也比较完美。长期以来,对于极限定理的研究所形成的机率论分析方法,影响着机率论的发展。同时新的极限理论问题也在实际中不断产生。
中心极限定理有着有趣的历史。这个定理的第一版被法国数学家棣莫弗发现,他在1733年发表的卓越论文中使用常态分配去估计大量抛掷硬币出现正面次数的分布。这个超越时代的成果险些被历史遗忘,所幸着名法国数学家拉普拉斯在1812年发表的巨着Théorie Analytique des Probabilités中拯救了这个默默无名的理论。拉普拉斯扩展了棣莫弗的理论,指出二项分布可用常态分配逼近。但同棣莫弗一样,拉普拉斯的发现在当时并未引起很大反响。直到十九世纪末中心极限定理的重要性才被世人所知。1901年,俄国数学家里雅普诺夫用更普通的随机变数定义中心极限定理并在数学上进行了精确的证明。如今,中心极限定理被认为是(非正式地)机率论中的首席定理。
定义
独立同分布的中心极限定理
设随机变数X1,X2,......Xn,......独立同分布,并且具有有限的数学期望和方差:E(Xi)=μ,D(Xi)=σ20(k=1,2....),则对任意x,分布函式

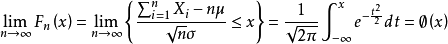
该定理说明,当n很大时,随机变数 近似地服从标準常态分配N(0,1)。因此,当n很大时,
近似地服从标準常态分配N(0,1)。因此,当n很大时,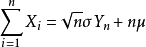 近似地服从常态分配N(nμ,nσ2).该定理是中心极限定理最简单又最常用的一种形式,在实际工作中,只要n足够大,便可以把独立同分布的随机变数之和当作正态变数。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。
近似地服从常态分配N(nμ,nσ2).该定理是中心极限定理最简单又最常用的一种形式,在实际工作中,只要n足够大,便可以把独立同分布的随机变数之和当作正态变数。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。

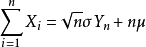
棣莫佛-拉普拉斯定理
设随机变数X(n=1,2,...,)服从参数为n,p(0<p<1)的二项分布,则对于任意有限区间(a,b)有

该定理表明,常态分配是二项分布的极限分布,当数充分大时,我们可以利用上式来计算二项分布的机率。
不同分布的中心极限定理
设X1,X2,......Xn是一列独立随机变数,它们的机率密度分别为 ,并有E(Xk)=μk,
,并有E(Xk)=μk, ,(k=1,2,...),令:
,(k=1,2,...),令:


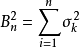

若对任意正数τ,有

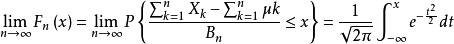
套用
中心极限定理在A/B测试中的套用
中心极限定理是机率论中最重要的一类定理,它支撑着和置信区间相关的T检验和假设检验的计算公式和相关理论。如果没有这个定理,之后的推导公式都是不成立的。
事实上,以上对于中心极限定理的两种解读,在不同的场景下都可以对A/B测试的指标置信区间判定起到一定作用。
对于属于常态分配的指标数据,我们可以很快捷地对它进行下一步假设检验,并推算出对应的置信区间;而对于那些不属于常态分配的数据,根据中心极限定理,在样本容量很大时,总体参数的抽样分布是趋向于常态分配的,最终都可以依据常态分配的检验公式对它进行下一步分析。
其他举例
1.某炮兵阵地对敌人的防御地段进行100次射击,每次射击中炮弹的命中数是一个随机变数,其期望为2,方差为1.69,求在100次射击中有180颗到220颗炮弹命中目标的机率。
解:设Xk表示第k次射击中的炮弹数,则E(Xi)=2,D(Xi)=1.69,且S100=X1+X2+…+X100,套用中心极限定理, 近似服从N(0,1),由题意
近似服从N(0,1),由题意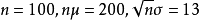 ,所以:
,所以:

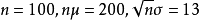
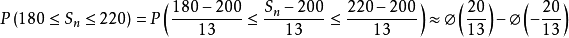
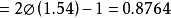
所以在100次射击中有180颗到220颗炮弹命中目标的机率为87.64%.
2.一个複杂系统由100个相互独立的元件组成,在系统运行时每个元件损坏的机率为0.1,为使系统正常工作,至少必须有85个元件工作,求系统的可靠度(正常工作的机率)。
解:以X表示100个元件中正常工作的元件数,则X~B(100,0.9),由二项分布的正态近似,


即正常工作的机率为95.25%.