闭线性运算元(closed linear operator)是一种特殊的线性运算元,常直接称为闭运算元。连续线性运算元必是闭运算元,但闭运算元不一定是连续运算元。根据闭图像定理可知,定义域是闭子空间的闭运算元是连续运算元。
基本介绍
- 中文名:闭线性运算元
- 外文名:closed linear operator
- 别名:闭运算元
- 等价条件:图像是闭集
- 出处:泛函分析
- 套用领域:鲁棒控制
定义
定义1(闭线性运算元)设X,Y均为Banach空间,T是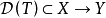 的线性运算元。对于任意的
的线性运算元。对于任意的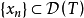 ,若由
,若由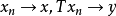 可得
可得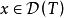 ,且
,且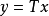 ,则称T为闭线性运算元,简称闭运算元。
,则称T为闭线性运算元,简称闭运算元。
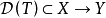
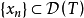
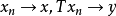
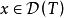
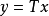
注:每个连续线性运算元T都可以将定义域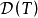 延拓到
延拓到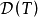 的闭包上,因此每个连续线性运算元T都可以看成是有闭定义域的,于是每个连续线性运算元必是闭运算元;但一般的闭线性运算元不一定是连续运算元(下面的例1证实了这一说法)。
的闭包上,因此每个连续线性运算元T都可以看成是有闭定义域的,于是每个连续线性运算元必是闭运算元;但一般的闭线性运算元不一定是连续运算元(下面的例1证实了这一说法)。
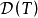
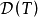
例1 考察微分运算元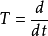 ,它是定义在
,它是定义在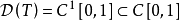 上,取值于
上,取值于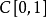 的线性运算元。取函式
的线性运算元。取函式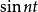 ,则
,则
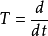
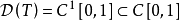
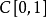
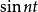
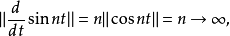
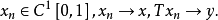
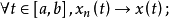
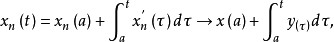
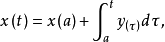
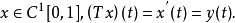
定义2(线性运算元的图像)令T是定义在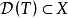 上到Y的线性运算元,称
上到Y的线性运算元,称
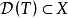
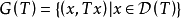
注: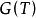 是
是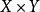 的线性子空间。
的线性子空间。
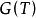
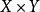
性质
上面定义的闭线性运算元有一个重要性质,即T的图象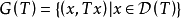 为乘积空间
为乘积空间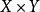 的一个闭线性子空间。定理描述为:
的一个闭线性子空间。定理描述为:
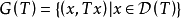
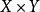
定理1 T是闭运算元的充分必要条件是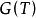 为闭集。
为闭集。
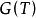
证明:(1)必要性 设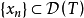 ,
,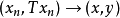 . 因为T是闭运算元,则
. 因为T是闭运算元,则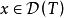 ,
,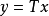 ,于是
,于是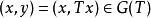 ,故
,故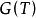 是闭集。
是闭集。
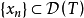
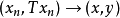
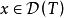
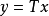
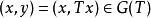
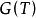
(2)充分性 设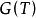 是闭的,若
是闭的,若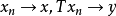 ,那幺
,那幺
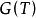
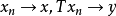
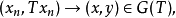
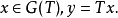
套用-闭图像定理
定理2(闭图像定理)设X,Y均为Banach空间,T是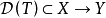 的线性运算元。
的线性运算元。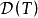 是X中的闭集。若
是X中的闭集。若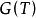 是
是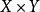 中闭集,则T是连续的。
中闭集,则T是连续的。
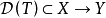
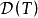
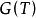
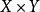
证:该定理的证明参见参考文献[1] 的291-292页。
由定理1可知,定理2还可叙述成:在定理2的条件下,若T是闭运算元,则T是连续的。因此定义域是闭子空间的闭运算元是连续运算元。
拓展
闭线性运算元原是泛函分析中的概念,后被引入鲁棒控制中讨论系统的不稳定摄动问题。经研究发现,控制系统中一个对象的传递函式P(s)(n×m阶实有理矩阵),若仅在有限功率谱输入与输出情况下考虑,实际上等于引入了一个从输入空间Hm2到输出空间Hn2的闭线性运算元,这一结论为在鲁棒控制中引入隔扑(Gap)概念讨论系统的不稳定摄动打下了基础。
