完备的赋范代数称为巴拿赫代数(Banach代数),它是泛函分析的一个重要分支,主要研究带有乘法的赋范线性空间的性质及其套用。
基本介绍
- 中文名:巴拿赫代数
- 外文名:Banach Algebras
- 概述:完备的赋范代数
- 本质:特殊的线性空间
- 重要概念:元素的谱
- 所属学科:数学
定义
代数
定义1 设 是一个线性空间,称
是一个线性空间,称 是一个代数,若:对
是一个代数,若:对 中任意两个元素
中任意两个元素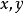 ,规定乘积
,规定乘积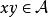 ,满足对
,满足对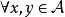 和任意数a,有
和任意数a,有



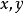
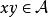
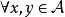
(1)结合律 x(yz)=(xy)z;
(2)分配律 x(y+z)=xy+xz,(x+y)z=xz+yz;
(3)a(xy)=(ax)y=x(ay).
注:1)设 是一个代数,如果存在
是一个代数,如果存在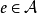 ,使得
,使得

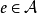
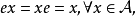


2)设 是一个代数,如果
是一个代数,如果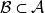 ,且
,且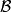 按
按 的线性运算及乘法仍是一个代数,则称
的线性运算及乘法仍是一个代数,则称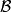 是
是 的一个子代数。
的一个子代数。

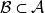
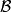

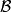

3)设 是一个代数,当
是一个代数,当 有单位元时,单位元必是唯一的。
有单位元时,单位元必是唯一的。


4)设 是一个有单位元的代数,
是一个有单位元的代数,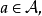 且存在
且存在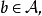 使得
使得

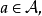
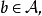
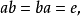

赋范代数
定义2 设 是一个赋范线性空间,同时又是一个代数,而且
是一个赋范线性空间,同时又是一个代数,而且

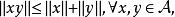

注:在赋范代数中,关于乘积範数的性质保证了乘法运算的连续性。实际上,当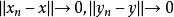 时,
时,
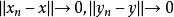
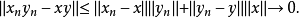
Banach代数
定义3 完备的赋范代数称为Banach代数。
举例
例1 设X是赋范线性空间,则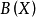 (由X到X的有界线性运算元全体)是一个有单位元的赋范代数,X上的恆等运算元I 即为其单位元。当X为Banach空间时,
(由X到X的有界线性运算元全体)是一个有单位元的赋范代数,X上的恆等运算元I 即为其单位元。当X为Banach空间时,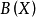 是Banach代数。
是Banach代数。
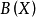
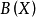
例2 设X是Banach空间,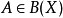 ,
,
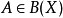
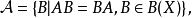


例3 设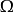 是紧拓扑空间,
是紧拓扑空间, 表示
表示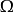 上连续函式全体,对
上连续函式全体,对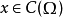 ,令
,令
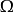

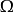
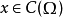
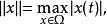

谱与谱半径
对于有限维线性空间上的线性变换,特徵值是一个十分重要的概念。这个概念拓广到一般的Banach代数中,就是元素的谱。(这里讨论的Banach代数是指复Banach代数。)
定义4 设 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,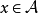 ,
,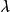 为複数,如果存在
为複数,如果存在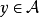 ,使得
,使得


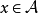
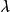
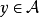
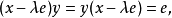
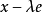
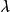
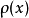
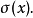
定义5 设 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,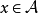 ,记
,记


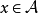
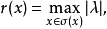
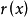
Banach代数的重要性质
定理1 设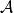 是具有单位元
是具有单位元 的Banach代数,则
的Banach代数,则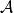 中可逆元全体是开集,且映射
中可逆元全体是开集,且映射
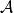

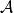
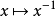
定理2 设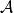 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,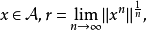 则
则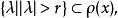 当
当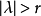 时,
时,
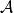

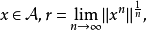
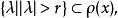
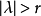
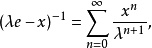
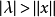
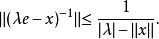
定理3 设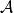 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,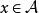 ,则
,则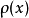 是开集。对
是开集。对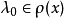 ,记
,记
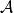

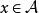
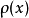
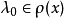
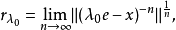
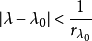
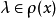

定理4 设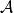 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,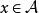 ,则
,则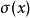 是闭集,且
是闭集,且
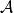

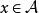
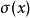
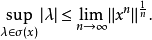
定理5 设 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,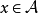 ,则谱半径
,则谱半径


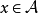
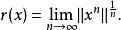
定理6 设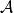 是具有单位元
是具有单位元 的Banach代数,
的Banach代数,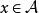 ,则
,则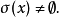
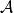

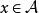
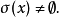
定理7 设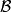 是Banach代数
是Banach代数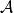 的闭子代数,
的闭子代数,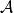 、
、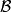 有相同的单位元,
有相同的单位元,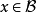 ,则
,则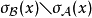 为开集。
为开集。
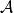
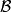
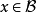
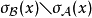
注:定理1-7的证明见参考文献[1]的59-64页。

