通过对信用评级流程,框架,基本要素及打分卡的研究,提出本文观点:信用风险分析的本质是处理不确定性,而关键是贝叶斯统计决策方法的运用。
信用风险度量主要包括以下步骤: 一是明确影响信用风险的主要因素; 二是获取影响因素的数据信息及变数的动态特徵; 三是构建和选择模型度量风险, 在此过程中, 机率论和统计方法的套用不可或缺。
目前国际上,信用风险度量方法不仅考察了违约机率的测度,而且探讨了信用等级转移矩阵的选择和比较。中国大公评级原理通过对偏离度的测量,确定债务信用风险级别,从已有文献中,可以发现在信用风险度量中的三个主要问题:第一,在变数选择和模型设定时都面临经验数据缺乏的问题;第二,无论是偏离度度量,还是违约机率度量,信用评级时都大量使用了专家意见或经验判断;第三,模型预测和比较都需要处理不确定性问题。贝叶斯方法提供了一种有效的风险预测手段,能够将主观估计与客观估计结合起来,并能随着资料的不断增加而不断进行预测,使得预测更加精确,它能够科学的使用专家意见等主观信息,在处理不确定性问题上具有一定的优势,已较为广泛的套用于信用风险度量领域。
基本介绍
- 中文名:大公国际评级原理-贝叶斯信用评估模型
- 别称:贝叶斯信用评估模型
- 提出者:路璐
- 提出时间:2015.7.29
- 套用学科:评估、预测、战略预测
- 适用领域範围:评估、预测、战略预测
- 适用领域範围:评估、预测、战略预测
2015年1月技术总结
——贝叶斯信用评估模型
研究院公用事业部 路璐
序言
通过对信用评级流程,框架,基本要素及打分卡的研究,提出本文观点:信用风险分析的本质是处理不确定性,而关键是贝叶斯统计决策方法的运用。
信用风险度量主要包括以下步骤: 一是明确影响信用风险的主要因素; 二是获取影响因素的数据信息及变数的动态特徵; 三是构建和选择模型度量风险, 在此过程中, 机率论和统计方法的套用不可或缺。
目前国际上,信用风险度量方法不仅考察了违约机率的测度,而且探讨了信用等级转移矩阵的选择和比较。中国大公评级原理通过对偏离度的测量,确定债务信用风险级别,从已有文献中,可以发现在信用风险度量中的三个主要问题:第一,在变数选择和模型设定时都面临经验数据缺乏的问题;第二,无论是偏离度度量,还是违约机率度量,信用评级时都大量使用了专家意见或经验判断;第三,模型预测和比较都需要处理不确定性问题。贝叶斯方法提供了一种有效的风险预测手段,能够将主观估计与客观估计结合起来,并能随着资料的不断增加而不断进行预测,使得预测更加精确,它能够科学的使用专家意见等主观信息,在处理不确定性问题上具有一定的优势,已较为广泛的套用于信用风险度量领域。
信用评级发展历史
1909 年, 着名评级公司穆迪的创始人在《铁路投资分析年刊》中首次提出信用评级的概念, 至今信用风险度量己走过100年的历程。结构模型和强度模型是传统信用风险度量模型的两种主要形式,前者利用资产负债的变数关係描述违约,后者利用特徵参数强度描述违约事件。
1970年提出通过更新技术修正后验机率预测信用风险,为后期贝叶斯多期动态模型的发展奠定了基础。再此之前,线性判别模型是度量信用风险的主要方法,通过赋予不同的指标权重综合评分判断信用等级,线性判别模型中的重要假定是不同等级的方差协方差矩阵相同, 且评分数据服从常态分配, 但这些假定过于严格,这种线性判别模型就是目前普遍用到的打分卡模型的前身。
贝叶斯信用风险度量模型与传统模型并不相同,在模型中既可以考虑资产价值的变动也可以涉及偏离距离变数, 具有更强的适应性和灵活性。
贝叶斯方法
传统的风险分析往往是预测各种事件可能发生的先验机率, 或者是根据历史资料的客观机率, 或者是採取专家的经验值(即主观机率)。然而, 设定先验分布是件困难的事情。因为许多决策问题的先验信息不够充分, 而先验分布又往往只能凭决策人所获得的先验信息对状态发生的机率作出主观估计, 因此设定的先验分布很难準确地反映客观真实情况。而贝叶斯推断则首先确定事件自然状态的先验机率, 然后根据先验机率进行初步决策。随着主体的运行成长, 不断的通过科学试验、调查、统计分析等分方法获得较为準确的补充信息, 根据这些补充信息, 重新修正对原有事件机率分布的估计。经过多次修正以后, 对事件的机率分布估计会越来越準确, 越来越符合实际情况。
一般, 通过试验并不能直接观察状态变数θ的值。只能观察到与θ有关的另外一个随机变数X的值。对于给定的θ, X的条件密度函式记作f(Xθ)。当似然函式f(Xθ)为已知时,可由损失函式L(θ,δ)求得风险函式R(θ,δ)的值。对于给定的先验密度f(θ), 又可由风险函式R(θ,δ)求得贝叶斯风险r(θ,δ)的值。贝叶斯分析是决策分析中的一种主要方法, 它是选择决策规则δ使贝叶斯风险最小。因此, 使用贝叶斯分析必须假设有先验密度和损失函式,而且人们能设定它们的值。
由此可见,贝叶斯方法具有如下优点:
1.对调查结果的可能性加以数量化的评价,而不像其他方法,对调查结果完全相信,或完全不相信。
2.由于任何调查结果都不可能是完全準确的,先验机率也不是完全可以相信的,而贝叶斯方法巧妙将这两种信息有机地结合起来。
3.它可以在风险分析中根据具体情况不断使用,使得风险分析逐步帖近实际,更加準确。
贝叶斯方法基本原理
贝叶斯估计
设θˋ是θ的估计量,由于θˋ与θ或多或少会有一些距离, 因而可以定义一个非负的二元函式L(θ,θˋ),称为在用θˋ估计θ时的损失函式,通常最常用的是二次损失函式:
L(θ, θˋ)=(1)
显然L(θ,θˋ)越小,表明θ估计越好,但是这里θ和θˋ(x1, x2,…,xn)都是随机变数, 因此这里所希望的“小”只能代表机率的意义。
由机率论可知, 样本与参数的联合分布密度函式为:
g(x1 , x2 , … , xn, θ)=g(x1 , x2 , …, xn θ)h(θ) (2)
则有:对于θ的一个估计值θˋ=θ ˋ(x1 , x2 , …, xn),
R(θˋ)= ∫Θ∫ΨL(θ, θˋ(x1 , x2 , …, xn))· g(x1 , x2 , …, xn|θ)h(θ)dx1dx2 …dxndθ (3)
这里Θ为参数空间, Ψ为样本空间, R(θˋ)称为估计量θˋ的贝叶斯风险,并称R(θ0 ˋ)为使贝叶斯风险达到最小的估计θˋ,
即R(θ 0ˋ)=minR(θˋ) (4)
为θ的贝叶斯估计。
为求得贝叶斯估计,将(3)式两边关于θˋ求导,并令其结果等于零,经整理计算得到θ的贝叶斯估计为:
θ 0 ˋ(x)= ∫ Θθh(θ|x)dθ (5)
其中:
h(θ|x) =h(θ|x1 , x2 , …, xn) =
h(θ|x)称为θ的后验机率密度。由此可知, 估计值θˋ与实际值θ之间的差距将随着后验机率不断调整,如果能不断的补充信息,不断的调整后验机率,则估计值将逐步接近实际值。对于风险分析而言, 即对风险的估计将越来越準确。
贝叶斯估计推广
假设f(x)为随机变数的常态分配密度函式,μ为x的均值。x1 , x2 , … , xn是x的n个随机样本,具有已知的精度r(r=1 /), x为样本均值。按照贝叶斯原理,如果x为随机变数, 则x的均值μ也是随机变数。假设μ的先验分布是一个常态分配,具有已知的均值μ′和精度t′, 则μ的后验分布也是一个常态分配,其均值μ″和精度t″分别为:
μ″= (6)
t″=t′+nr (7)
式中,
由式(6)和式(7)可以知道,后验均值μ″是先验均值μ′和样本均值x的一个加权平均, 而其权重正是各种精度t′和nr,而且当样本规模n较大时,样本精度r较大(样本标準差较小)时, nr也较大,从而使样本均值有较大的权。μ的后验分布的表达式(7)特别简单,随着观测次数n的增大正比于样本精度r而增加,而与x1无关。因而,随着观测次数的增加,μ的后验分布越来越集中于后验均值的周围,而其均值将取决于观测值xi。
贝叶斯信用评估模型
项目评级中,会有众多决定因素和因子,如俄罗斯天然气工业公司风险管理系统有500多因子,大公评级原理把确定偿债能力的众多因素分在偿债环境,财富创造能力,偿债来源三大要素里,并且提出了偏离度的定义,综合衡量和调节偿债能力。这些因素和因子会随着时间和形势发展不断变化,直接影响评级结果,如俄罗斯天然气工业公司可以提供给分析师的是截止到半年前的财务资料和报表,对评级工作产生很大的约束和限制。用贝叶斯方法将大公评级原理的三大要素放在同一测算平台进行评估。评估过程将分别对三大要素进行分析:偿债环境如何;财富创造能力是多大;偿债来源是多少,除此之外,还要计算偏离度,以便衡量偿债能力,再据此进行预测、决策与控制,从而提前预警主体的债务风险。
下面以分析偿债来源的子项初级偿债来源为例进行说明。用一定时期(以月为例)预计实现初级偿债来源构成序列,考察每月预计初级偿债来源的情况,建立数学模型推出初级偿债来源的机率分布。由于每月的初级偿债来源xi要受到盈利、经常性收入、债务收入、可变现资产、外部支持、外汇收入、货币发行等很多方面的影响, 所以它是一个随机变数。假设xi是具有均匀分布的随机变数,则其和x1+x2 +…+xn的极限分布将是一个常态分配,其均值为μ,方差为。然后根据数据确定其参数,从而得出每单位时期的初级偿债来源的估计。
分析步骤如下:
(1)採集样本。收集以往资料, 计算样本均值, 样本方差, r=1 /。
(2)确定先验机率分布参数。评级分析师根据其经验和所掌握的信息,判断每月的初级偿债来源为多少。然后将所得估算值进行平均,并计算其误差範围,这样就可得到先验机率分布参数μ′和精度t′。
(3)进行后验机率分布推断。利用样本信息和先验机率信息, 进行贝叶斯推断。根据式(6)和式(7),计算的初级偿债来源的后验均值μ″和精度t″。
(4)给定置信度λ,P=1-λ, 查常态分配表,UP =C,则初级偿债来源均值μ的区间估计为[μ″-C*S,μ″+C*S] 。
(5)继续补充新信息,或调整先验信息,或增加新的样本,套用上述模型,信息越多、样本越大,均值的估计就越準确。
贝叶斯方法在评级项目中的套用
求某企业初级偿债来源,已知前9月企业初级偿债来源如图1所示。同时7名分析师对初级偿债来源进行估算,其评估结果如表2所示。
表1 前9月企业初级偿债来源的情况(满为100)
日期(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
初级偿债来源 | 49 | 47 | 53 | 45 | 57 | 60 | 52 | 54 | 49 |
表2 分析师估算企业初级偿债来源的情况(满为100)
专家 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
评估值 | 55 | 57 | 52 | 59 | 58 | 54 | 60 |
(1)根据所得样本, 可算出:
样本均值 =51.778,
样本方差=23.194, S样=4.816,
样本精度r=1 /样 =0.0043。
(2)计算先验参数:
均值 =56.43,
方差=8.286
精度t=0.12。
(3)进行后验机率分布推断:
初级偿债来源的后验均值
μ″= ==52.879
初级偿债来源的精度 t″=t′+nr=0.507
初级偿债来源的方差 =1/t″=1.97
(4) 令置信度λ=0.05, P=1-λ=0.95,查常态分配表,UP =C=1.96, 则初级偿债来源的均值μ的置信区间为:
μ″-C*S样≤ μ≤ μ″+C*S样
52.879 -1.96*4.816 ≤ μ≤ 52.879 +1.96*4.816
43.44 ≤ μ≤ 62.32
即: 初级偿债来源落入[ 43.44, 62.32]的机率为95%。
(5)若又得到以往类似企业的初级偿债来源的资料如表3所示:
表3 分析师估算企业初级偿债来源的情况(满为100)
专家 | 1 | 2 | 3 | 4 | 5 | 6 |
评估值 | 53 | 52 | 56 | 61 | 57 | 59 |
进一步修正有关参数, 原有的后验机率分布参数变为先验分布参数, 再综合新收集到的样本信息进行后验机率推断。
此时, 先验机率分布参数为:均值μ′=52.879, 精度t′=0.507
样本有关参数为:
样本均值 =56.33,
样本方差=11.867, S样=3.44,
样本精度r=1 /样 =0.084。
重新进行后验分布推断:
后验均值μ″==54.6
后验精度t″=t′+nr=1.011
后验方差δ2 =1/t″=0.99
给定置信度λ=0.05, 则初级偿债来源的均值μ的置信区间为: μ∈ [47.86, 61.34]。
可以看出, 增加了新信息后, 初级偿债来源的置信区间比以前更集中了。
初级偿债来源分析是测算偿债能力的环节之一。偿债环境、偿债来源和财富创造能力三大要素都可以按此方法进行测算。由于三大要素髮生的动态性,分析应不断进行,不断将当期出现的新信息补充到分析中去,以使得分析结果更贴近实际,反应企业状况。
贝叶斯专家评估系统
在评级领域里,标準普尔开发的智慧型专家评估系统命名为S&PCBRS,其主要任务是对公司发行的证券进行评级;建立正确的评级标準。该专家系统具有以下特徵:评级中的课题分类;神经分类机的学习和测验;专家分数的比较;运用神经网路Couter-Propagation词形变化。标普的专家评估系统準确率高达84%。
由于贝叶斯原理,方法和模型的複杂性局限了评级工作,从而设计了贝叶斯专家评估系统,以便分析师广泛套用。贝叶斯专家评估系统是一种在特定领域内具有专家水平解决问题能力的程式系统。它能够有效地运用专家多年积累的有效经验和专门知识,通过模拟专家的思维过程,解决需要专家才能解决的问题。贝叶斯专家评估系统可以在信息不全的情况下,对部分未知的状态用主观机率估计,然后用贝叶斯公式对发生机率进行修正,最后再利用期望值和修正机率做出最优决策。系统解决了分析工作量大,主观性强,实施效果不稳定问题,提高风险分析师决策的效率,实现风险评估自动化,为科学使用专家意见主观经验提供了有效途径。
本评估系统的基本工作流程是,分析师通过人机界面回答系统的提问,推理机将分析师输入的信息与知识库中各个规则的条件进行匹配,并把被匹配规则的结论存放到综合资料库中。最后,评级系统将得出最终结论呈现给分析师。
贝叶斯决策理论方法是统计模型决策中的一个基本方法,其基本思想是:
- 已知类条件机率密度参数表达式和先验机率;
- 利用贝叶斯公式转换成后验机率;
- 根据后验机率大小进行决策分类。
贝叶斯专家评估系统的函式基础是:
系统知识库建模: M=<H,S,G,P,VH,VS>
其中 H={H1,....Hn}-假设集合;
S= {S1,....Sm}-状态集合;
G=G(X,U,P+,P-) –加权二部图的顶点 X=(H, S), 圆弧 U , 圆弧机率为 P+ и P-;
圆弧U(Si,Hj)–表示状态集合 Si和假设集合 Hj,的关係,遵循«如果 Si, 就Hj»;
圆弧 U(Si,Hj)在知识库机率为P+ij=P(Si|Hj)–当假设Hj正确,那幺机率表现为Si ;
P-ij=P(Si|Hj)–当假设Hj错误,那幺症状为Si;
P={P1,....Pn} –实验机率假设;
VH和VS -用自然语言描述假设和状态.
所有机率区间在[0,1]。
评估作业系统的函式关係是:
P(Hj| Si)=Pj*P+ij/(Pj*P+ij+(1-Pj)*P-ij),
P(Hj| Si)=Pj*(1- P+ij)/(1-Pij+Pj*(P-ij-P+ij)),
Csi=∑|P(Hj|Si)-P(Hj|!Si) |,其中Csi–是状态Si的量值;
Ii–相对于状态Si的排序。
评估系统由人机互动界面、知识库、推理机、解释器、综合资料库、知识获取等6个部分构成。综合资料库包含求解问题的世界範围内的事实和断言。知识库包含所有用“如果:〈前提〉,于是:〈结果〉”形式表达的知识规则。推理机的任务是运用控制策略找到可以套用的规则。这些部分建立了支持评级流程的自动系统。
建立评估系统得系统静态结构,系统动态结构,以及工艺开发流程。
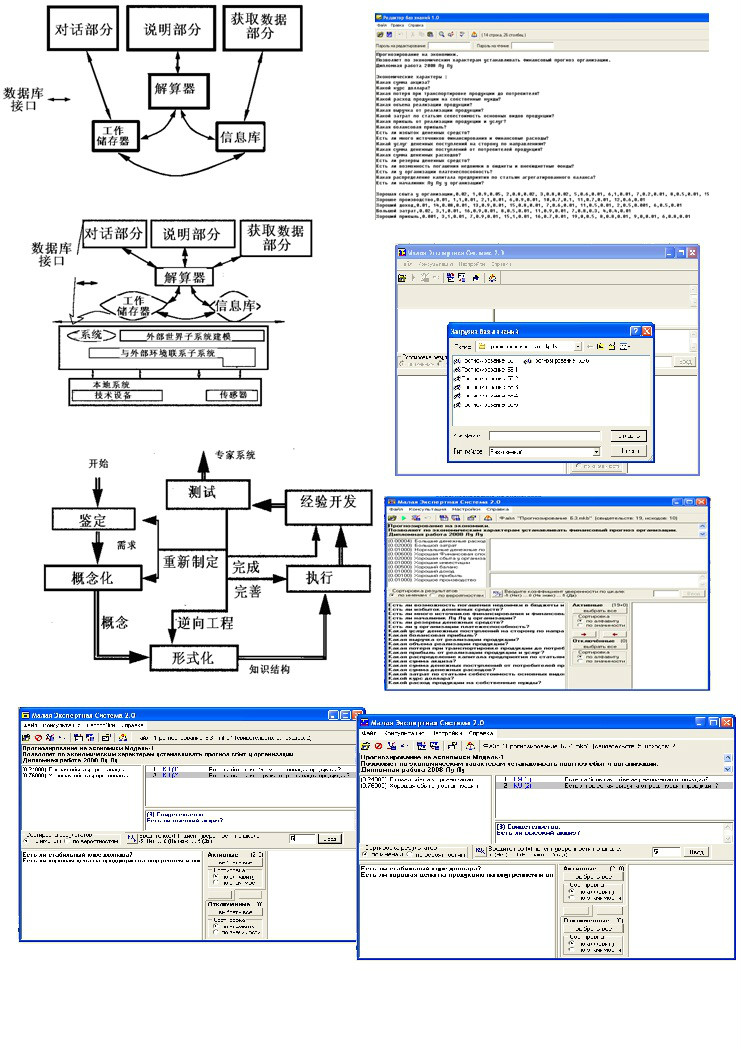
评估系统静态结构图,如下:
评估系统动态结构图,如下:
评估系统工艺开发图,如下:
评估系统人机交流的操作平台的开发设计。
知识库编写视窗,如下:
导入知识库视窗,如下:
评估过程视窗,如下:
结论视窗,如下:
结论导出视窗,如下:
贝叶斯专家评估系统应具备以下功能:
⑴ 存储解题所需的知识。
⑵ 储初始数据和推理过程中涉及的各种信息。
⑶ 据输入的数据,利用已有的知识,按照一定的推理策略,解决当前的问题,并能控制和协调整个系统。
⑷ 够对推理过程、结论和系统自身的行为做出必要的解释,便于分析师的理解和接受。
⑸ 供机器获取知识的路径,可以修改、扩充和完善知识库。
⑹ 供分析师接口,理解并满足分析师的各种要求。
关于贝叶斯专家评估系统的具体操作和套用,将在日后有机会时解释。
结语
分析了贝叶斯理论,基于贝叶斯方法构建评估模型,并根据先验机率或者专家经验,实现对未知因素的量化计算。同时,进行了实际案例推算,计算结果可供分析师进行参考。随着添加的历史信息的增多与经验的累积,估算越接近实际值,这样能让分析师在评估时减少失误和降低损失。从分析的结果可发现,本方法可按大公评级原理测算影响偿债能力的三大要素,从而实现对主体的评级。
公用事业部
二〇一五年一月十五日