它有一定的规律性，排列如下(构成图)，像上面的1、3、6、10、15等等这些能够表示成三角形的形状的总数量的数，叫做三角形数。

一定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为三角形数。比如10个点可以组成一个等边三角形，因此10是一个三角形数：

x

x　x

x　x　x

x　x　x　x

x　x　x　x x

开始个18个三角形数是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153、171……（OEIS中的数列A000217）

第n个三角形数的公式是 或者 。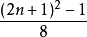

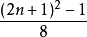
第n个三角形数是开始的n个自然数的和。

所有大于3的三角形数都不是质数。

开始的n个立方数的和是第n个三角形数的平方（举例：1 + 8 + 27 + 64 = 100 =10²）

所有三角形数的倒数之和是2。

任何三角形数乘以8再加1是一个平方数。

一部分三角形数（3、10、21、36、55、78……）可以用以下这个公式来表示：n × (2n + 1)；而剩下的另一部分（1、6、15、28、45、66……）则可以用n × (2n - 1)来表示。

一种检验正整数x是否三角形数的方法，是计算：。

如果n是整数，那幺x就是第n个三角形数。如果n不是整数，那幺x不是三角形数。这个检验法是基于恆等式8Tn + 1 = S²n + 1.

特殊的三角形数

55、5,050、500,500、50,005,000……都是三角形数。

第11个三角形数（66）、第1111个三角形数（617,716）、第111,111个三角形数（6,172,882,716）、第11,111,111个三角形数（61,728,399,382,716）都是回文式的三角形数，但第111个、第11,111个和第1,111,111个三角形数不是。

和其他数的关係

四面体数是三角形数在立体的推广。

两个相继的三角形数之和是平方数。

三角平方数是同时为三角形数和平方数的数。

三角形数属于一种多边形数。

所有偶完美数都是三角形数。

任何自然数是最多三个三角形数的和。高斯发现了这个规律。他在1796年7月10日在日记中写道：EYPHKA! num = Δ + Δ + Δ

o n=1 s=1

o o n=2 s=3

o o o n=3 s=6

o o o o n=4 s=10

o o o o o n=5 s=15

根据自然数列的求和公式，对于第n项的三角形数，可以得到其计算公式为：。

1)前n个三角形数的和:T(n)=s(1)+s(2)+…+s(n)

由，

得到:.。

2)判断一个数是否为三角形数:对任给一个正整数K，则若为三角形数,有:得:n*(n+1)=2K。

从而:[即2K开根号]<n+1;这样就得到了一个n，如果这个n满足:则说明K是三角形数。

具体:你注意到了吗，商店橱窗里的罐头盒一般都是这样排列的。它们按照一定的规律排成了三角形。想一想：能不能把9个圆点按上面的规律排成一个三角形？9是不是三角形数？再想一想：能不能把25个圆点按上面的规律排成一个三角形？25是不是三角形数？为了能方便地看出规律，我们把三角形数改排成图。观察这些三角形数，你发现它们有什幺规律吗？原来三角形数是从l开始的连续自然数的和。l是第一个三角形数，3是第二个三角形数，6是第三个三角形数，10是第四个三角形数，15是第五个三角形数……那幺，第七个三角形数就是：1+2+3+4+5+6+7=28；第九个三角形数就是：1+2+3+4+5+6+7+8+9=45；第十个三角形数就是：1+2+3+…+10=55；第100个三角形数就是：1+2+3+…+100=5050。

1.55、5050、500500、50005000……都是三角形数。

2.第11个三角形数（66）、第1111个三角形数（617716）、第111111个三角形数（6172882716）、第11111111个三角形数（61728399382716）都是回文式的三角形数，但第111个、第11111个和第1111111个三角形数不是。

3.三角形数还有一个规律，就是：如果将所有边形的数都整整齐齐地由左到右画在表格里，你就会发现，每一列的数间隔都一样，而且均为前一列的三角形数，例如：

4.比如10个点可以组成一个等边三角形，因此10是一个三角形数：

一开始的18个三角形数是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153、171、190、210、231、253……

一个三角数乘以九再加一仍是一个三角数。

三角数的个位数字不可能是2、4、7、9，数字根不可能是2、4、5、7、8。

三角数的二倍的平方根取整，是这个三角数的序数。

第n个三角形数的公式是。

第n个三角形数是从1开始的n个自然数的和。

所有大于3的三角形数都不是质数。

开始的n个立方数的和是第n个三角形数的平方（举例：1 + 8 + 27 + 64 = 100 = 10）。

所有三角形数的倒数之和是2。

任何三角形数乘以8再加1是一个平方数。

一部分三角形数（3、10、21、36、55、78……）可以用以下这个公式来表示：{\displaystyle n*(2n+1)}；而剩下的另一部分（1、6、15、28、45、66……）则可以用{\displaystyle n*(2n-1)}来表示。

一种检验正整数x是否三角形数的方法，是计算：

如果n是整数，那幺x就是第n个三角形数。如果n不是整数，那幺x不是三角形数。这个检验法是基于恆等式