分块矩阵是高等代数中的一个重要内容，是处理阶数较高的矩阵时常採用的技巧，也是数学在多领域的研究工具。对矩阵进行适当分块，可使高阶矩阵的运算可以转化为低阶矩阵的运算，同时也使原矩阵的结构显得简单而清晰，从而能够大大简化运算步骤，或给矩阵的理论推导带来方便。有不少数学问题利用分块矩阵来处理或证明，将显得简洁、明快。
分块矩阵是一个矩阵， 它是把矩阵分别按照横竖分割成一些小的子矩阵 。 然后把每个小矩阵看成一个元素。
基本介绍
- 中文名：分块矩阵
- 外文名：partitioned matrix
- 类别：矩阵
- 学科：高等数学
- 特殊：分块对角矩阵，分块上三角矩阵
- 相关：求解线性方程组
定义
将一个矩阵用若干条横线和竖线分成许多个小矩阵，将每个小矩阵称为这个矩阵的子块，以子块为元素的形式上的矩阵称为分块矩阵。
例如，
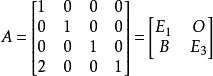
其中E1，E3分别表示1阶、3阶单位矩阵，O表示1×3的零矩阵，而
。
同一个矩阵可以有多种不同的分块方法，从而形成不同的分块矩阵。例如上例的矩阵也可分成也可分成
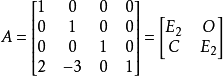
其中E2表示2阶单位矩阵，O表示2阶零矩阵，而
。
运算规则
加法
设
，
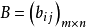，用同样的方法对A，B进行分块，即
，
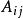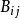为同型矩阵，则
。
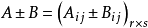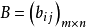
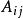
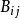
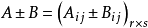
数乘
设
，k是任意数，定义分块矩阵
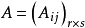与k的数乘为
。
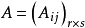
乘法
设A是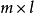
阶矩阵，B是
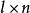阶矩阵，即A的列数=B的行数，分块
，
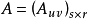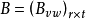，即A的列分块法=B的行分块法。
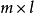
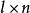
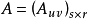
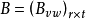
则A与B的乘积
是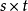
阶分块矩阵，
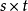
转置
设矩阵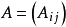
是
阶分块矩阵，
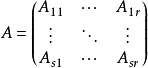，则
。
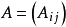
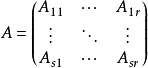
特殊分块矩阵
分块对角矩阵
设A为n阶方阵，若A的分块矩阵在非主对角线上的子块皆为零矩阵，且在主对角线上的子块都是方阵，即
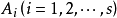
性质：
①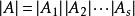
；
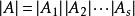
②若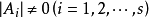
，则A可逆，且
；
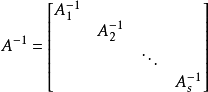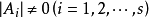
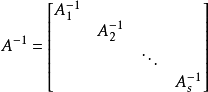
③同结构的準对角矩阵的和、差、积、数乘及逆仍是準对角矩阵，且运算表现为对应子块的运算。
分块上下三角矩阵
对方阵进行分块后，主对角线上的子块矩阵都是方阵，主对角线以下（以上）的子块矩阵都是零矩阵，即
性质：
①同结构的分块上（下）三角形矩阵的和（差）、积（若乘法运算能进行）仍是同结构的分块矩阵。
② 数乘分块上（下）三角形矩阵也是分块上（下）三角形矩阵。
③ 分块上（下）三角形矩阵可逆的充分必要条件是的主对角线子块都可逆；若可逆，则的逆阵也是分块上（下）三角形矩阵。
④ 分块上（下）三角形矩阵对应的行列式：
。