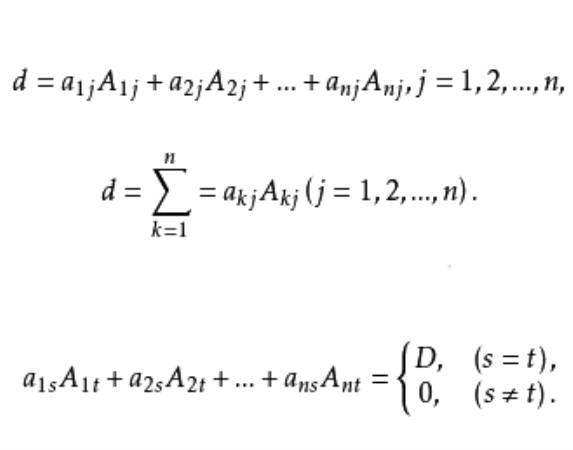行列式依列展开(expansion of a determinant by a column)是计算行列式的一种方法,设a1j,a2j,…,anj (1≤j≤n)为n阶行列式D=|aij|的任意一列中的元素,而A1j,A2j,…,Anj分别为它们在D中的代数余子式,则D=a1jA1j+a2jA2j+…+anjAnj称为行列式D的依列展开。
基本介绍
- 中文名:行列式依列展开
- 外文名:expansion of a determinant by a column
- 所属学科:数学
- 所属问题:高等代数(行列式)
- 基本介绍:计算行列式的一种方法
基本介绍
设a1j,a2j,…,anj(1≤j≤n)为n阶行列式D=|aij|的任意一列中的元素,而A1j,A2j,…,Anj分别为它们在D中的代数余子式,则D=a1jA1j+a2jA2j+…+anjAnj称为行列式D的依列展开。
例如,在一个三阶行列式D中,划去元素aij(i=1, 2,3; j=1, 2,3)所在的第i行和第j列的所有元素,剩下的元素按照它原有的位置得到的一个二阶行列式称为元素aij的余子式,记作Mij。而将(-1)Mij称为元素aij的代数余子式,记作Aij,即Aij=(-1)Mij。例如

行列式可按行或列展开,于是每个行列式可以表成它的某一行(或某一列)的每个元素与它对应元素的代数余子式乘积的和,即
D= ai1Ai1+ ai2Ai2+ ai3Ai3 (i= 1, 2,3) , (1)
D= a1jA1j+ a2jA2j+ a3jA3j (j=1,2, 3), (1')
我们把类似(1)式的展开称为行列式的依行展开式,把(1')式称为行列式的依列展开式。
相关定理
定理1 (行列式按列展开规则) n阶行列式d等于它的任意一列元素与它们对应的代数余子式之积的和,即


定理2如果行列式D的第s列各元素与第t列各元素的代数余子式对应相乘后再相加,则当s≠t时,其和为零。因此有

此定理也可以叙述为:n阶行列式(n>1)的某列的元素与另一列的对应元素的代数余子式乘积的和等于零。
例题解析
【例1】计算:
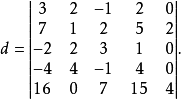
解:d中第5列零元素较多,应从这一列入手。
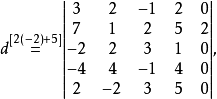

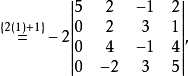
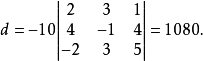
说明在行列式计算中,我们经常利用行列式的展开把n阶行列式转化为n-1阶行列式,通过降阶逐步变为低阶行列式后进行计算,但行列式按某一行或列展开时,只有在该行或列的元素有较多的零时,才能起到减少计算量的作用,因此往往先运用“化零”后进行“降阶”,利用行列式性质降低行列式阶数,然后计算行列式之值的方法称为降阶法,例1就是降阶法的一例。