莫尔一库侖强度理论(Mohr Coulomb theory)由德国工程师莫尔(Christian Otto Mohr，1835—1918)于1900年提出。该理论认为，材料发生剪断破坏的原因主要是某一截面上的切应力达到强度极限值，但也与该面上的正应力有关。如截面上存在压应力，则与压应力大小有关的材料内摩擦力将阻止截面的滑动；如果截面上存在拉应力，则截面将容易滑动，因此剪断不一定发生在最大剪应力的截面上。在三向应力状态下，如果不考虑中间应力σ₂，对材料破坏的影响，则一点处的最大切应力或较大切应力可由最大和最小主应力σ₁和σ₃所画的应力圆决定。材料在破坏时的应力圆称“极限应力圆”，根据σ₁和σ₃ 的不同比值(如单轴拉伸、单轴压缩、纯剪，各种不同大小应力比的三轴压缩试验等)，可作出一系列极限应力圆，这些应力圆的公共包络线（右图所示）便是材料破坏的临界线。

极限应力圆的包络线

法国物理学家库侖(Charles Augustinde Coulomb，1736—1806)于1773年提出，假定强度极限值是同一平面上法向应力的线性函式，则包络线可简化为直线，常称“莫尔—库侖理论”或“库侖强度理论”。莫尔强度理论能较全面地反映岩石和土的强度特性(如岩石和土的抗拉强度远小于抗压强度)。该理论适用于脆性材料，也适用于塑性材料。

为了简化计算，将莫尔应力圆包络线简化为直线（右图b），即岩石材料的破坏条件与土力学中所採用的相同，也可用库侖方程式表示，即：

莫尔库伦强度破坏条件

式中：c—为岩石凝聚力；ψ—岩石内摩擦角。

由右图b可得：

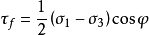
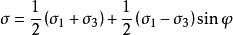
由上述公式可得：

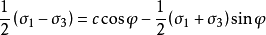
这一方程式常称为莫尔—库侖破坏强度方程式或莫尔—库侖破坏强度条件。