代数扩张，是指在抽象代数中，一个域扩张（通常记作）被称作代数扩张，若且唯若每个的元素都是在上代数的，即：满足一个係数布于的非零多项式。反之则称超越扩张。

设为任意的域扩张，可以看作是上的向量空间。

定义为其维度，称作这个扩张的次数。有限次数的扩张（简称有限扩张）都是代数扩张；反之，给定一个代数扩张，则里的任一元素都落在一个有限子扩张内，因此一个代数扩张可表作有限子扩张的归纳极限。

一种重要的域扩张。其特徵为p的域F的任意扩张K/F，Ω是K的代数闭包，若K与：

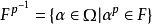
在F上是线性分离的，则称K/F是可分扩张。当F是完备域时，F上任何扩张都是可分扩张。当K/F是代数扩张时，若α∈K在F上的最小多项式是可分多项式，则称α是(F上的)可分代数元(简称F上可分元)。若K中每个元均为F上可分元，则称K是F上可分扩张。若K/F有一个超越基S，使得K是可分的，则称S是可分超越基。若K/F有这样一个可分超越基，则称此扩张K/F是可分生成的。完备域上的有限生成扩张均为可分生成扩张。可分扩张具有传递性。当K/F是有限生成，而且是可分扩张时，K/F是可分生成的。反之，可分生成的扩张必然是可分扩张。

代数闭包是实线性空间中的集合的代数意义下的闭包。设A为实线性空间X中的集合，A的代数闭包是指这样的点b∈X的全体：存在h∈X，对于任何ε>0，存在λ∈[0，ε]，使得b+λh∈A。A的代数闭包常记为acl(A)。如果A=acl(A)，那幺A称为代数闭集。它也是X在以代数开集为开集的拓扑意义下的闭集，即代数闭集的余集必定是代数开集；反之亦然。代数闭包的概念在叙述凸集分离定理时也起重要作用。

有的文献定义代数闭包时，要求对于任何λ∈(0，ε)都有b+λh∈A.这时代数闭集就不再是代数开集的余集。但当A是多于一点的凸集时，由这两种定义得到的代数闭包是相同的。

纯超越扩张是一类重要的超越扩张。设扩域K在F上的超越基为S，若K=F(S)，则称此域扩张为纯超越扩张，K为F的纯超越扩域。此时，K与F上一组未定元X的多项式环F[X]的分式域(商域)F(X)同构，其中X与S的基数相等。一般地，设K是F的任一扩域，若其超越基为S，则F(S)是F的纯超越扩域，K为F(S)的代数扩域。这样，一个域扩张可分成两种特殊的域扩张来研究，即FF(S)K。超越次数为1的纯超越扩张称为单超越扩张。

正则扩张(regular extension)一类特殊的可分扩张。设F^是域F的代数闭包，K是F的扩域。若K与F^在F上是线性分离的，则称K/F为正则扩张。K/F成为正则扩张，若且唯若F在K中是代数封闭的，同时K/F是可分扩张。F上的纯超越扩张都是正则扩张。特别地，当K与F的可分闭包F^_S在F上为线性分离时，称K/F为準素扩张。K/F成为正则扩张，等价于K/F是準素扩张，同时又是可分扩张。

正则扩张的主要性质有：

性质一：正则扩张是可传递的：如果F/E和E/K都是正则扩张，那幺F/K也是正则扩张；

性质二：如果F/K是正则扩张，那幺对任意在F和K之间的E有E/K也是正则扩张；

性质三：L/K是正则扩张若且唯若L有限生成的每个子域在K上是正则的；

性质四：代数闭合域的任何扩展都是正则的；

性质五：一个扩展是正则的若且唯若它是可分离的；

性质六：一个域的纯粹超验的扩展是正则的。