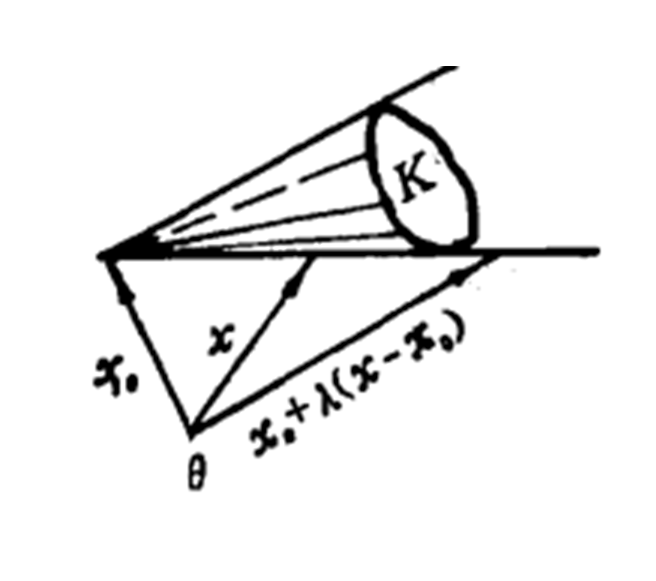
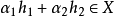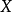一类特殊的凸集被称之为凸锥,它有极其重要的性质和套用。既是锥又是凸集的点集称之为凸锥。常见的凸锥包括:二维平面中的半射线、整个n维欧式空间等。凸锥中有一个重要的定理,凸锥分离定理。
基本介绍
- 中文名:凸锥
- 外文名:Convex cone
- 基础知识:凸集、锥
- 常见凸锥:二维平面中半射线、n维欧式空间
- 重要定理:凸锥分离定理
- 套用学科:凸理论基础
基础知识
凸集
设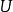 为
为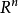 中的点集,当
中的点集,当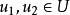 ,对任意的
,对任意的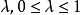 ,点
,点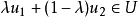 ,即连线
,即连线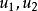 的整个线段
的整个线段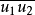 上的点都属于
上的点都属于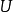 ,则称
,则称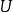 为凸集。
为凸集。
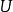
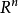
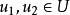
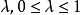
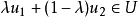
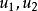
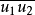
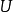
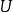
锥
设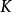 是
是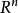 中的点集,当
中的点集,当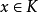 ,对任意的
,对任意的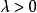 ,点
,点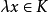 ,即由原点出发过
,即由原点出发过 的半射线上的点都属于
的半射线上的点都属于 ,则称K为锥。
,则称K为锥。
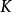
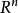
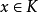
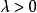
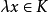


定义
设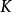 是
是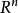 中的点集,若点集
中的点集,若点集 既是锥又是凸集时,即当
既是锥又是凸集时,即当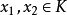 时,对任意不同时为零的
时,对任意不同时为零的 ,点
,点 ,则称
,则称 为凸锥。
为凸锥。
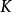
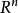

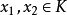



性质
简单性质
(1)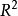 中的半射线是锥且是真凸锥。
中的半射线是锥且是真凸锥。
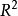
(2)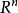 中的集
中的集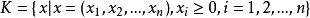 是锥并且是真凸锥。
是锥并且是真凸锥。
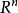
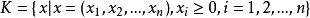
凸集分离定理
设 是
是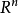 中的两个凸锥,且
中的两个凸锥,且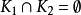 ,即两个凸锥无公共点,那幺存在一个超平面,将把
,即两个凸锥无公共点,那幺存在一个超平面,将把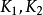 分离,即存在一个矢量
分离,即存在一个矢量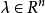 使得下面的不等式成立:
使得下面的不等式成立:

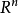
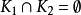
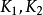
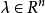
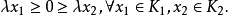
典例
例1
整个空间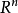 是凸锥。
是凸锥。
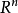
例2
设 和
和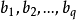 是p+q个已知的n维向量,则满足条件
是p+q个已知的n维向量,则满足条件

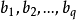
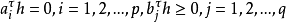
证明:对任意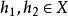 和任意两个不同时为零的实数
和任意两个不同时为零的实数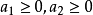 ,有:
,有:
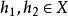
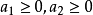
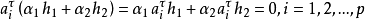
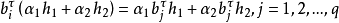
因此,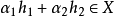 ,
,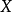 为凸锥。
为凸锥。