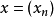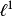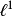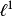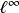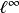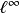在数学分析中,巴拿赫极限(英语:Banach limit)指的是定义在全体有界复序列组成的巴拿赫空间上,对每个巴拿赫空间中的序列和複数满足一定条件的连续线性泛函。
基本介绍
- 中文名:巴拿赫极限
- 外文名:Banach limit
- 领域:数学分析
介绍
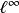
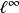
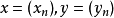
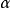
(1)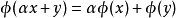 (线性);
(线性);
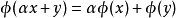
(2)若对每个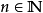 有
有 ,则
,则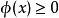 (正定性);
(正定性);
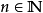

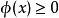
(3)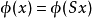 ,其中S是移位运算元,定义为
,其中S是移位运算元,定义为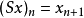 (移位不变性);
(移位不变性);
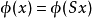
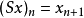
(4)若x是收敛序列,则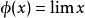 .
.
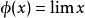
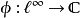
因此,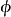 是对连续线性泛函
是对连续线性泛函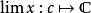 的延拓,其中
的延拓,其中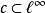 是
是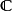 中收敛到某个极限的全体序列组成的复向量空间。进而可以视为发散级数论中的一个可和法。
中收敛到某个极限的全体序列组成的复向量空间。进而可以视为发散级数论中的一个可和法。
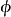
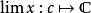
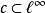
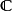
换句话说,巴拿赫极限是对通常意义下极限概念的延拓,并且是线性、移位不变、正定的。可以对某个序列找到两个巴拿赫极限,使得各自作用下得到两个不同的值,我们称这类序列的巴拿赫极限不是唯一确定的。
作为上述性质的一个推论,每个实值巴拿赫极限也满足:
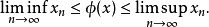
巴拿赫极限的存在性通常需要套用哈恩-巴拿赫定理证明(分析学方法),也可以套用超滤子(这种方法在集合论的讨论中出现得更频繁)。这些证明都一定会用到选择公理(即所谓的非构造证明)。
几乎收敛
某些不收敛的级数在巴拿赫极限的作用下是唯一确定的。 例如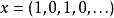 ,注意到
,注意到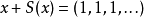 是常序列,并且
是常序列,并且
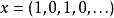
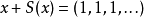
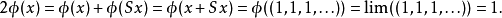
因此对每个巴拿赫极限而言,它以1/2为极限。
我们将每个巴拿赫极限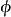 下有相同的
下有相同的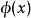 的有界序列 x称为几乎收敛的。
的有界序列 x称为几乎收敛的。
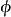
Ba 空间
在 中给定收敛序列
中给定收敛序列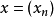 ,如果考虑对偶
,如果考虑对偶 ,x通常的极限并不由
,x通常的极限并不由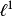 的某个元素给出。实际上
的某个元素给出。实际上 是
是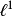 的连续对偶空间(对偶巴拿赫空间);反过来,
的连续对偶空间(对偶巴拿赫空间);反过来,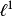 虽然能诱导出
虽然能诱导出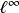 中的连续线性泛函,但并不是全部。每个
中的连续线性泛函,但并不是全部。每个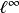 上的巴拿赫极限都是
上的巴拿赫极限都是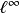 的对偶巴拿赫空间中的一个元素,但不在
的对偶巴拿赫空间中的一个元素,但不在 中。
中。 的对偶叫做ba空间,由一切自然数集子集的σ-代数上有限可加(符号)测度组成,或者等价地说是由每个自然数集的Stone–Čech紧化上的波莱尔(符号)测度组成。
的对偶叫做ba空间,由一切自然数集子集的σ-代数上有限可加(符号)测度组成,或者等价地说是由每个自然数集的Stone–Čech紧化上的波莱尔(符号)测度组成。