在泛函分析中，巴拿赫定理是一个极为重要的工具。它允许了定义在某个向量空间上的有界线性运算元扩张到整个空间，并说明了存在“足够”的连续线性泛函，定义在每一个赋范向量空间，使对偶空间的研究变得有趣味。
这个定理以汉斯·哈恩和斯特凡·巴拿赫命名，他们在1920年独立证明了这个定理。
基本介绍
- 中文名：巴拿赫定理
- 外文名：Hahn–Banach theorem
- 学科：数学
内容简介
巴拿赫定理(Banach theorem)表明函式的全变差与指标函式的(L)积分之间关係的定理。设f (x)是巨，司上的连续函式，m与M分别为f(二)在压，司上的最小值与最大值，N(y) (m镇y镇M)是方程.fCx)=y的根的个数，称N(户为巴拿赫指标函式，则N(必在[m,M]上(L)可测。
表述
定理的最一般的表述需要一些準备。给定标量域（实数或複数）上的一个向量空间V，一个函式称为次线性的，如果：
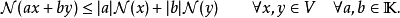
可以很容易证明，V上的每一个範数和每一个半範数都是次线性的。其它的次线性函式也可以是很有用的。
哈恩-巴拿赫定理说明，如果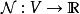
是一个次线性函式，
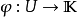是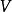
的子空间U上的一个线性泛函，满足：
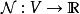
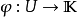
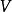
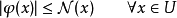
那幺存在φ到整个空间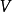
的一个线性扩张
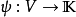，也就是说，存在一个线性泛函ψ，使得：
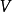
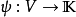
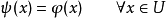
以及：
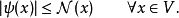
扩张ψ一般不是由φ唯一指定的，定理的证明也没有给出任何求出ψ的方法：在无穷维空间
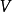
我们可以把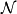
的次线性条件稍微减弱，只需要：
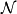
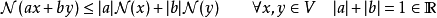
根据（Reed and Simon, 1980）。这揭示了哈恩-巴拿赫定理与凸性的密切联繫。