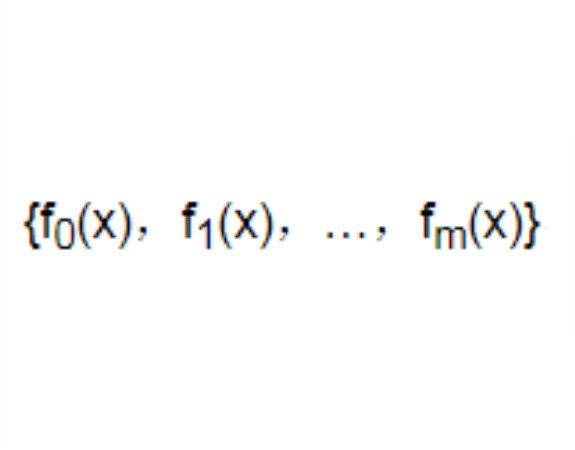斯图姆定理(Sturm theorem)是确定实係数多项式实根个数的一个重要定理,设f(x)是实係数n(n≥1)次多项式,令f0(x)=f(x),f1(x)=f′(x),则由带余除法,f0(x)=f1(x)q1(x)+r1(x).令f2(x)=-r1(x),对f1(x)与f2(x),由带余除法有f1(x)=f2(x)q2(x)+r2(x),再令f3(x)=-r2(x),并对f2(x)与f3(x)作带余除法,如此继续下去,得多项式序列:f0(x),f1(x),…,fs(x),…,fm(x),称为f(x)的斯图姆序列,斯图姆定理是:设f(x)是实係数多项式,且f(x)无重根,f0(x),f1(x),…,fm(x)是f(x)的斯图姆序列,若a<b,f(a)≠0和f(b)≠0,则序列f0(a),f1(a),…,fm(a)的变号数V(a)与序列f0(b),f1(b),…,fm(b)的变号数V(b)的差V(a)-V(b)恰是f(x)在区间(a,b)内实根的个数,斯图姆(C.-F.Sturm)在1829年的论文《论数字方程解》中,深入地讨论了代数方程根的隔离,引入了斯图姆序列的概念,给出了斯图姆定理。
基本介绍
- 中文名:斯图姆定理
- 外文名:Sturm theorem
- 所属学科:数学
- 所属问题:高等代数(多项式)
- 发现者:斯图姆(J.C.F.Sturm, 1803-1855)
基本介绍
斯图姆定理是判断实係数多项式方程实根个数的定理。给出实係数多项式方程
f(x)=a0xn+…+an-1x+an=0, a0≠0,
令f0(x)=f(x),f1(x)=f′(x),用f1(x)除f0(x)得商q1(x)及余式-f2(x),一般地有
fk-1(x)=fk(x)qk(x)-fk+1(x),(k=1,2,…,m),
直到fm+1(x)≡0为止,得到m+1个多项式序列
{f0(x),f1(x),…,fm(x)},
称为以f0及f1为基的斯图姆序列,当x=a时,
{f0(a),f1(a),…,fm(a)}
是一个数列。若其中两个相邻数符号相反就称为一次变号,记此数列变号次数为Va,若f(a)≠0,f(b)≠0,且数列
{f0(b),f1(b),…,fm(b)}
的变号次数为Vb,则f(x)=0在[a,b]内共有Va-Vb个不相同的实根,设最后非零函式fm(x)没有实根,则f(x)=0的实根都是单根,若fm(x)=0有实根,则这些根都是f(x)=0的重根,其重数为fm(x)=0内的重数加1,这就是斯图姆定理的内容。当a=-∞,b=+∞时,则得f(x)=0实根个数;当(a,b)内只有一个根且b-a很小,则可解决实根的隔离问题。
相关说明
(1)斯图姆分离定理是一个关于二阶线性微分方程零解的定理:设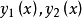 为方程y"+q(x)y=0的两个线性无关的解。若
为方程y"+q(x)y=0的两个线性无关的解。若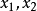 分别使
分别使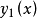 为零,则
为零,则 在
在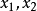 之间至少有一个零点。
之间至少有一个零点。
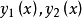
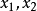
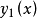

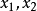
(2)斯图姆比较定理是一个重要定理:已知两个方程y"+q1(x)y=0,z"+q2(x)z=0,且在(a, b)内q2(x)≥q1(x), 则在第一个方程任一解的两个零点之间,至少有第二个方程每个解的一个零点。
斯图姆定理可用于研究满足齐次边界条件的方程y"+q(x)y=λy的斯图姆——柳维尔问题。
1829年,法国数学家斯图姆得出了求实係数代数方程在已知区间上的实根个数的简单方法——斯图姆方法,而这方法的依据就是斯图姆定理,刘维尔说:“由于这一巨大的发现,斯图姆立即简化并且完整了代数的原理,用新的解法充实了它们。”
斯图姆(J.C.F.Sturm, 1803-1855)是原籍瑞士的法国数学家。