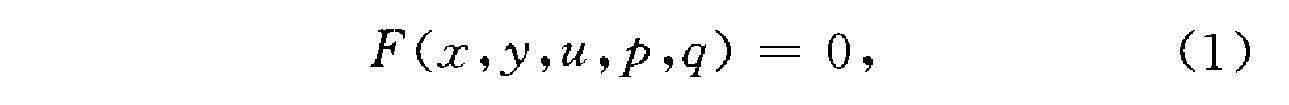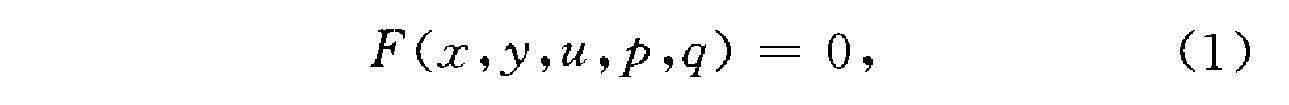一阶非线性偏微分方程(non-linear partial dif- ferential equation of first order)一阶的完全非线 J胜偏微分方程.两个自变数的一阶非线性偏微分方 程的一般形状是

其中p=ur,q=u,,,F为五个变元的二次连续可微函 数，F墓+F李}0，方程(1)给出待求的积分曲面 u=u(二，y)的法向量((p ,q,-1)在(二，y,u)空间中每 点尸处应满足的条件.所以积分曲面在尸点处的切 平面形成通过尸的一族单参数平面族，此单参数的 平面族的包络是以尸为顶点的一个锥面，这个锥面 称为蒙日锥.蒙日锥的母线方向称为特徵方向.在 (x,y,u)空间中以特徵方向为其每点处方向的曲线 称为蒙日曲线.在拟线性方程的情形，蒙日锥退化为 蒙日轴.