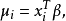广义线性模型[generalize dlinear model]线性模型的扩展,通过联结函式建立回响变数的数学期望值与线性组合的预测变数之间的关係。其特点是不强行改变数据的自然度量,数据可以具有非线性和非恆定方差结构。是线性模型在研究回响值的非常态分配以及非线性模型简洁直接的线性转化时的一种发展。
基本介绍
- 中文名:广义线性模型
- 外文名:generalized linear model
- 适用範围:数理科学
简介
假设因变数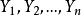 是 n 个独立观测,服从指数型分布,即其有密度函式:
是 n 个独立观测,服从指数型分布,即其有密度函式:
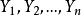
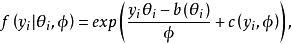
其中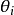 和
和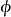 为参数,
为参数,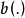 和
和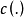 为函式。
为函式。
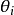
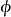
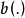
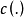
假设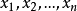 为对应于
为对应于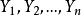 的 p 维自变数 X 的观测值。记
的 p 维自变数 X 的观测值。记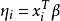 ,其中
,其中 为
为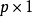 未知参数向量。假设
未知参数向量。假设 并且
并且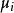 与
与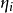 具有关係
具有关係
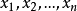
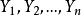
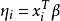

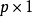

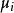
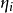
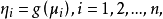
称如此定义的模型为广义线性模型,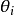 称为自然参数,
称为自然参数,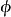 称为离散参数,称
称为离散参数,称 为联繫函式(连线函式)。
为联繫函式(连线函式)。
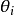
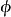

联繫函式
联繫函式确定了广义线性模型的均值结构,对于不同的数据类型,不同的联繫函式的选取就产生了不同的广义线性模型。比如,对0-1变数数据,即实验结果只有两种情况。将全部试验数据分成 n 个组,第 i 组有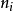 个数据.它们对应的自变数都为
个数据.它们对应的自变数都为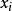 在这个数据中,假设对应的因变数取值为 1 的数据个数为
在这个数据中,假设对应的因变数取值为 1 的数据个数为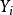 假设
假设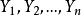 相互独立,并记因变数取1的机率为
相互独立,并记因变数取1的机率为 .如果
.如果 与
与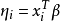 具有如下关係
具有如下关係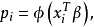 其中
其中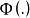 为标準常态分配函式,则称该广义线性模型为机率单位模型(probit model)。
为标準常态分配函式,则称该广义线性模型为机率单位模型(probit model)。
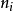
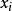
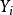
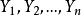


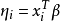
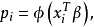
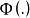
如果联繫函式为 ,且满足
,且满足

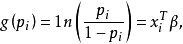
则称该广义线性模型为对数单位模型(logit model)。再如,对计数数据(比如,在一定时间内某随机事件发生的次数),如果假设观测数据服从泊松分布.即

则当联繫函式满足