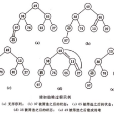
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
基本介绍
- 中文名：堆
- 外文名：heap
- 定义：一类数据结构的统称
释义
堆（英语：heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：
- 堆中某个节点的值总是不大于或不小于其父节点的值；
- 堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆是非线性数据结构，相当于一维数组，有两个直接后继。
堆的定义如下：n个元素的序列{k1,k2,ki,…,kn}若且唯若满足下关係时，称之为堆。
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)
若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。由此，若序列{k1,k2,…,kn}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。
STL
堆的STL包含于
#include "algorithm"
头档案中。
堆的STL支持以下的基本操作:
make_heap(first, last, comp);
建立一个空堆；
push_heap(first, last, comp);
向堆中插入一个新元素；
top_heap(first, last, comp);
获取当前堆顶元素的值；
sort_heap(first, last, comp);
对当前堆进行排序；
算法思想
不必将值一个个地插入堆中，通过交换形成堆。假设一个小根堆的左、右子树都已是堆，并且根的元素名为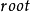
，其左右子节点为
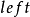和
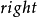，这种情况下，有两种可能：
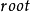
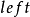
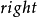
（1）
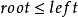并且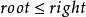
，此时堆已完成；
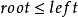
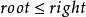
（2）
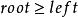或者
，此时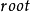 应与两个子女中值较小的一个交换，结果得到一个堆，除非 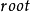仍然大于其新子女的一个或全部的两个。这种情况下，我们只需简单地继续这种将 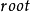“拉下来”的过程，直至到达某一个层使它小于它的子女，或者它成了叶结点。
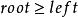
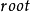
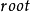
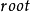
筛选法
首先将要排序的所有关键码放到一棵完全二叉树的各个结点中（这时的完全二叉树并不具备堆的特性）。显然，所有的结点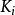
都没有子女结点，因此以这样的 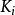为根的子树已经是堆，然后从 的结点Ki开始，逐步把以为根的子树排成堆，直到以K0为根的子树排成堆，就完成了建堆过程。
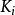
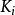
在考虑将以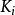 为根的子树排成堆时，以
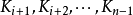为根的子树已经是堆，所以这时如果有
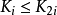和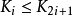
，则不必改变任何结点的位置，以 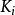为根的子树就已经是堆；否则就要适当调整子树中结点的位置以满足堆的定义。由于Ki的左、右子树都已经是堆，根结点是堆中最小的结点，所以调整后 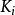的值必定是原来
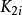和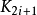
中较小的一个。假设
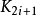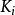较小，将 与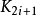 交换位置，这样调整后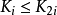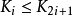，，并且以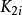 为根的子树原来已经是堆，不必再作任何调整，只有以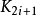为根的子树由于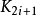的值已经发生变化（与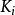交换了），所以有可能不满足堆的定义（当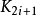的左、右子树已经是堆）。这时可重複上述过程，考虑将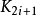以为根的子树排成堆。如此一层一层递推下去，最多可以一直进行到树叶。由于每步都保证将子树中最小的结点交换到子树的根部，所以这个过程是不会反馈的。它就像过筛一样，把最小的关键码一层一层选择出来。
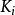
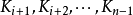
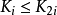
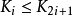
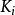
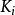
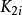
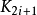
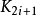
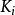
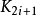
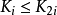
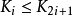
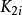
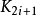
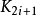
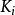
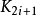
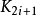
建堆效率
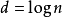
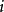
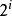
由于堆有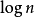
层深，插入结点、删除普通元素和删除最小元素的平均时间代价和时间複杂度都是
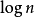
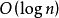
操作实现
在程式中，堆用于动态分配和释放程式所使用的对象。在以下情况中调用堆操作：
1.事先不知道程式所需对象的数量和大小。
2.对象太大，不适合使用堆叠分配器。
堆使用运行期间分配给代码和堆叠以外的部分记忆体。
传统上，作业系统和运行时库随附了堆实现。当进程开始时，作业系统创建称为进程堆的默认堆。如果没有使用其他堆，则使用进程堆分配块。语言运行时库也可在一个进程内创建单独的堆。（例如，C 运行时库创建自己的堆。）除这些专用堆外，应用程式或许多载入的动态程式库 (DLL) 之一也可以创建并使用单独的堆。Win32 提供了一组丰富的 API用于创建和使用专用堆。有关堆函式的优秀教程，请参阅 MSDN 平台 SDK 节点。
当应用程式或 DLL 创建专用堆时，这些堆驻留于进程空间中并且在进程範围内是可访问的。某一给定堆分配的任何数据应为同一堆所释放。（从一个堆分配并释放给另一个堆没有意义。）
在所有虚拟记忆体系统中，堆位于作业系统的虚拟记忆体管理器之上。语言运行时堆也驻留在虚拟记忆体之上。某些情况下，这些堆在作业系统堆的上层，但语言运行时堆通过分配大的块来执行自己的记忆体管理。绕开作业系统堆来使用虚拟记忆体函式可使堆更好地分配和使用块。
典型的堆实现由前端分配器和后端分配器组成。前端分配器维护固定大小块的自由列表。当堆收到分配调用后，它尝试从前端列表中查找自由块。如果此操作失败，则堆将被迫从后端（保留和提交虚拟记忆体）分配一个大块来满足请求。通常的实现具有每个块分配的开销，这花费了执行周期，也减少了可用存储区。
Windows NT的实现（Windows NT 4.0 版及更高版本）使用 127 个从 8 到 1,024 位元组不等的 8 位元组对齐块的自由列表和 1 个混合列表。混合列表（自由列表【0】）包含大小超过 1,024 位元组的块。自由列表包含在双向连结表中连结在一起的对象。默认情况下，进程堆执行合併操作。（合併操作是组合相邻的自由块以生成更大的块的操作。）合併操作花费了额外的周期，但减少了堆块的内部碎片。
单个全局锁可防止多执行绪同时使用堆。此锁主要用于保护堆数据结构不受多执行绪的任意访问。当堆操作过于频繁时，此锁会对性能造成负面影响。
代码实现
c++实现
#pragma oncetemplate<class T>class JBMinHeap{private: //申请堆空间 T *_minHeap = NULL; int _index,_maxSize;public: JBMinHeap(int maxSize) { _maxSize = maxSize; _minHeap = new T[_maxSize]; _index = -1; } JBMinHeap(JBMinHeap &h) { _index = h._index; _maxSize = h._maxSize; _minHeap = new T[_maxSize]; for (int i = 0;i<_maxSize) { *_minHeap[i] = *h._minHeap[i]; } } ~JBMinHeap() { delete[]_minHeap; } //获取整个最小堆的头部指针 T * getMinHeap() { return _minHeap; } //判断堆是不是空的 bool isEmpty() { return _index == -1; } bool add(T x) { if (isFull()) { return false; } _index++; _minHeap[_index] = x; return true; } bool isFull() { return _index == _maxSize; } //堆进行向下调整 void adjustDown(int index); //队进行向上调整 void adjustUp(int index); //建堆运算 void createMinHeap() { if (isEmpty()) { return; } for (int i = (_index-1)/2;i >-1;i--) {//直接从倒数第二层 逐层向下调整 adjustDown(i); } }};template<class T>void JBMinHeap<T>::adjustDown(int index) { if (isEmpty()) { return; } while (index<_index) { T temp = _minHeap[index];//将当前索引的位置的值保存下来 int oneC = 2 * index + 1;//获取到两个孩子的位置 int twoC = 2 * index + 2; if (oneC == _index) {//若第一个孩子是整个堆最后一个位置 则直接执行交换操作并结束执行 _minHeap[index] = _minHeap[oneC]; _minHeap[oneC] = temp; return; } if (twoC >_index) {//如果第二个孩子的索引位置越界 结束执行 return; } if (_minHeap[oneC] <= _minHeap[twoC]) {//正常情况的数据互动执行 if (temp > _minHeap[oneC]) { _minHeap[index] = _minHeap[oneC]; _minHeap[oneC] = temp; index = oneC; } else {//如果该处索引值已经是比两个孩子小 则结束循环 index = _index; } } else { if (temp > _minHeap[twoC]) { _minHeap[index] = _minHeap[twoC]; _minHeap[twoC] = temp; index = twoC; } else { index = _index; } } }}template<class T>void JBMinHeap<T>::adjustUp(int index) { if (index > _index) {//大于堆的最大值直接return return; } while (index>-1) { T temp = _minHeap[index]; int father = (index - 1) / 2; if (father >= 0) {//如果索引没有出界就执行想要的操作 if (temp < _minHeap[father]) { _minHeap[index] = _minHeap[father]; _minHeap[father] = temp; index=father; } else {//若果已经是比父亲大 则直接结束循环 index = -1; } } else//出界就结束循环 { index = -1; } }}VB.net实现
Public Class Priority_QueueFriend Element() As IntegerFriend point As Integer ReadOnly Property Top As IntegerGetTryReturn Element(1)Catch ex As ExceptionReturn 0End TryEnd GetEnd PropertyReadOnly Property Size As IntegerGetReturn pointEnd GetEnd PropertyReadOnly Property Empty As BooleanGetIf point = 0 Then Return TrueReturn FalseEnd GetEnd Property Sub push(ByVal _ele_val As Integer)point += 1Element(point) = _ele_valDim Now As Integer = pointDim Nxt As Integer = Now / 2While (Now <> 1 AndAlso Element(Now) > Element(Nxt))Swap(Element(Now), Element(Nxt))Now = NxtNxt /= 2End WhileEnd SubSub pop()Dim now As Integer = 1 Element(1) = Element(point)point -= 1 While (1) Dim left As Integer = 0Dim right As Integer = 0 If (now * 2 <= point) Thenleft = Element(now * 2)End IfIf (now * 2 + 1 <= point) Thenright = Element(now * 2 + 1)End If If (right = left And right = 0) ThenExit SubEnd If If (Element(now) < left OrElse Element(now) < right) ThenIf left > right ThenSwap(Element(now), Element(now * 2))now *= 2ElseSwap(Element(now), Element(now * 2 + 1))now *= 2now += 1End IfElseExit WhileEnd IfEnd While End Sub Sub New(ByVal _size As Integer)ReDim Element(_size)point = 0End SubProtected Overrides Sub Finalize()MyBase.Finalize()End Sub End Class