在量子力学里,表达粒子的量子态的波函式必须满足归一条件(归一化,英语:be normalized),也就是说,在空间内,找到粒子的机率必须等于1。这性质称为归一性。
基本介绍
- 中文名:归一条件
- 外文名:be normalized
- 别称:归一化
- 学科:量子力学
- 领域:量子力学
- 定义:找到粒子的机率必须等于1
定义
在量子力学里,表达粒子的量子态的波函式必须满足归一条件(归一化,英语:be normalized),也就是说,在空间内,找到粒子的机率必须等于1。这性质称为归一性。用数学公式表达,

归一化导引
一般而言,波函式 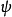 是一个複函数。可是,
是一个複函数。可是,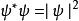 是一个实函式,大于或等于0,称为“机率密度函式”。所以,在区域
是一个实函式,大于或等于0,称为“机率密度函式”。所以,在区域 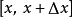 内,找到粒子的机率
内,找到粒子的机率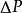 是
是
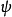
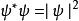
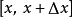
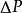

既然粒子存在于空间,机率是1。所以,积分于整个一维空间:
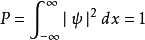
假若,从解析薛丁格方程而得到的波函式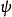 ,其机率P是有限的,但不等于1,则可以将波函式
,其机率P是有限的,但不等于1,则可以将波函式 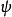 乘以一个常数,使机率P等于1。或者,假若波函式内,已经有一个任意常数,可以设定这任意常数的值,使机率P等于1。
乘以一个常数,使机率P等于1。或者,假若波函式内,已经有一个任意常数,可以设定这任意常数的值,使机率P等于1。
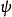
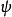
归一化恆定性
给予一个归一化的波函式。随着时间的变化,波函式也会改变。假若,随着时间改变的波函式不再满足归一条件,则势必要重新将波函式归一化。这样,归一常数A变得含时间。很幸运地,满足薛丁格方程的波函式的归一性是恆定的.设定波函式 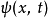 满足薛丁格方程与归一条件:
满足薛丁格方程与归一条件:
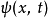
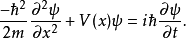
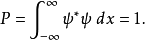
假若,归一性是恆定的,则机率P不含时间。为了显示这一点,先计算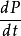 :
:
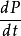
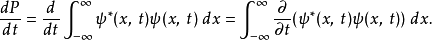

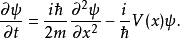


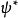
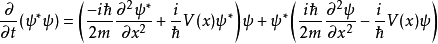
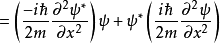
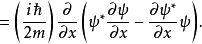
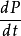

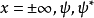
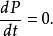
实例
在一维空间内,束缚于区域  内的一个粒子,其波函式是
内的一个粒子,其波函式是


其中,k是波数,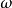 是角频率,A是任意常数。
是角频率,A是任意常数。
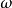
计算能够使波函式归一化的常数值A。将波函式代入:
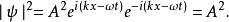
积分于整个粒子存在的区域:
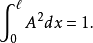
稍加运算,
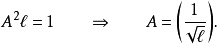
归一化的波函式是:


