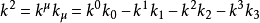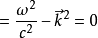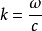波矢是波的矢量表示方法。
基本介绍
- 中文名：波矢量
- 外文名：wave vector
- 别称：波矢 波向量
- 套用学科：物理学 晶体学
- 适用领域範围：狭义相对论
定义
波矢是波的矢量表示方法。波矢是一个矢量，其大小表示波数（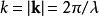
），其方向表示波传播的方向。
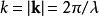
波矢在狭义相对论背景下可定义为四维矢量。
波矢有两种常见的定义，区别在于振幅因子是否乘以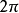
，两种定义分别用于物理学和晶体学以及它们的相关领域。
物理学定义
理想的一维行波遵循如下方程：
其中：
x为位置；
t为时间；
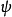
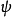
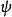
A是波的振幅（振动的峰值）；
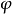
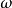
k是波数，与波长成反比，由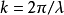
求出。
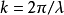
此波在+x方向上行进，相速度为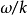
。
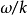
推广到三维情况下，方程为：
其中：
r是三维空间中的位置矢量；
k是波矢。
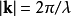
晶体学定义
在晶体学中，描述相同的波的方程略有不同。在一维和三维情况下的方程分别为：
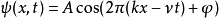
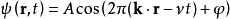
不同点在于：
晶体学定义使用了频率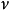
，而不是角频率
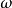，由公式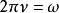
，二者可以相互转换。这种置换主要反映了在晶体学中的常见套用。
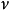
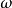
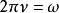
波数k以及波矢k的定义方式不同。此处的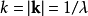
，而在物理学定义中，
。
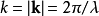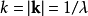
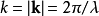
狭义相对论
接近单色光的波包可以由波矢
準确描述，若明确的改写成共变和反变形式，则
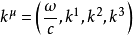
于是波矢的大小为
