四维矢量，是在狭义相对论里，四维矢量 (four-vector) 是实值四维矢量空间里的矢量。这四维矢量空间称为闵可夫斯基时空。四维矢量的分量分别为时间与三维位置。在闵可夫斯基时空内的任何一点，都代表一个事件，可以用四维矢量表示。套用洛伦兹变换，而不是伽利略变换 ，我们可以使对于某惯性参考系的四维矢量，经过平移，旋转，或递升（相对速度为常数的洛伦兹变换），变换到对于另一个惯性参考系的四维矢量。所有这些平移，旋转，或递升的集合形成了庞加莱群( Poincaré group)。所有的旋转，或递升的集合则形成了洛伦兹群(Lorentz group)。
基本介绍
- 中文名：四维矢量
- 外文名：Four-dimension vector
- 数学性质：两个事件之间的矢量差
- 动力学：物体运动的速度随着时间改变
- 套用学科：数学
- 所属领域：数学和物理学
数学性质
四维位移定义为两个事件之间的矢量差。在时空图里，四维位移可以用一只从第一个事件指到第二个事件的箭矢来表示。当矢量的尾部是坐标系的原点时，位移就是位置。关于四维矢量的理论，通常提到的是位移。
透过洛伦兹变换，给予一个事件对于某惯性参考系的四维坐标，即可计算出这事件对于另外一个惯性参考系的四维坐标。这是个很优良的物理性质。当研究物理现象时，所涉及的四维矢量，最好都能够具有这优良的性质。这样，可以使得数学分析更加精緻犀利。
透过洛伦兹变换，给予一个事件对于某惯性参考系的四维坐标，即可计算出这事件对于另外一个惯性参考系的四维坐标。这是个很优良的物理性质。当研究物理现象时，所涉及的四维矢量，最好都能够具有这优良的性质。这样，可以使得数学分析更加精緻犀利。
在计算这四维矢量对于时间的导数时，若能选择固有时为时间变数，则求得的四维矢量仍旧具有这优良的性质。因为，固有时乃是个不变数；改换惯性参考系不会改变不变数。
在闵可夫斯基时空内的任何一点，都可以用四维矢量（一组标準基底的四个坐标）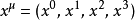
来表示；其中，上标
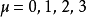标记时空的维数次序。称这四维矢量为“坐标四维矢量”，又称“四维坐标”，定义为
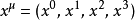
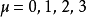
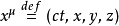
其中，c 是光速， t是时间，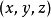
是位置的三维直角坐标。
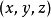
为了确使每一个坐标的单位都是长度单位，定义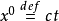
。
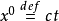
“四维位移”定义为两个事件之间的矢量差。在时空图里，四维位移可以用从第一个事件指到第二个事件的箭矢来表示。当矢量的尾部是坐标系的原点时，位移就是位置。四维位移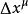
表示为
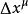
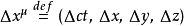
带有上标的四维矢量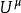
称为反变矢量，其分量标记为
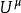
假若，标号是下标，则称四维矢量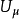
为协变矢量。其分量标记为
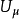
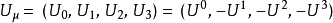
在这里，闵可夫斯基度规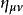
被设定为
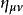
採用爱因斯坦求和约定，则四维矢量的协变坐标和反变坐标之间的关係为
闵可夫斯基度规与它的“共轭度规张量”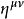
相等：
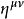
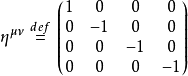
动力学
假设一个物体运动于闵可夫斯基时空。相对于实验室参考系，物体运动的速度随着时间改变。对于每瞬时刻，选择与这物体同样运动的惯性参考系，称为静止参考系。相对于这静止参考系，这物体的速度为零。随着物体不断地改变运动速度与方向，新的惯性参考系也会不断地改换为静止参考系。随着这些不断改换的静止参考系所测得的时间即为固有时，标记为 。这就好像给物体挂戴一只手錶，随着物体的运动，手錶也会做同样的运动，而手錶所纪录的时间就是固有时。
能量-动量关係式：
使用质能方程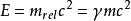 
，
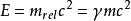
四维动量可以表示为：
。
四维动量与自己的内积为（即p的平方内积）：
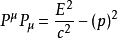
改以四维速度来计算内积：
所以，能量-动量关係式为：
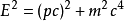
电磁学
四维电流密度
在电磁学里，四维电流密度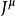
是一个四维矢量，定义为
其中，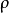
是电荷密度，
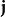是三维电流密度。
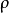
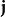
电荷守恆定律能以三维矢量表示为
这定律也能以四维电流密度表示为
从这方程，可以推论四维电流密度的四维散度等于零。