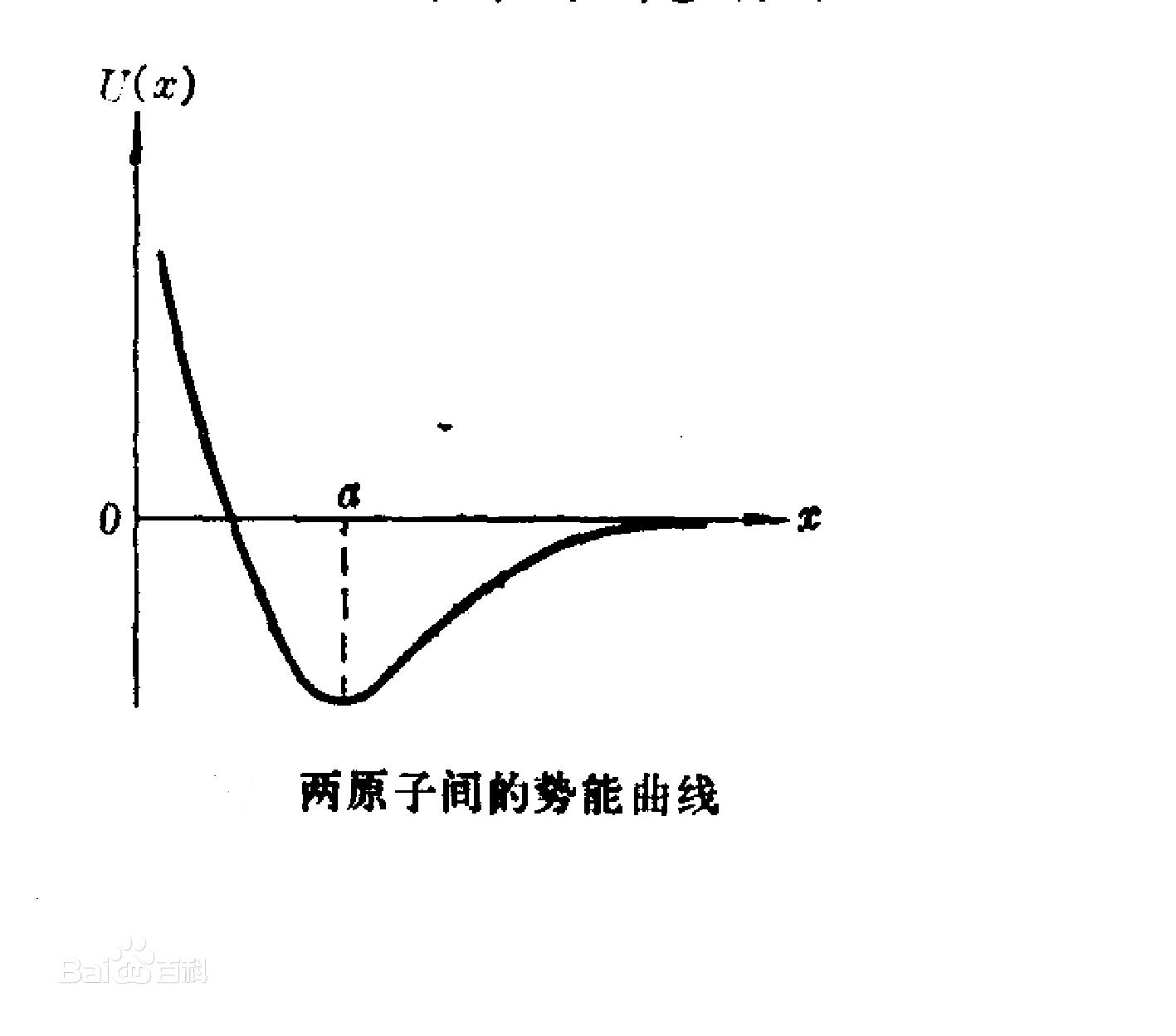
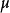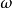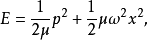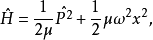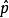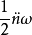线性谐振子是物理学中一个重要的模型,许多在平衡点附近振动的物理问题都可简化为线性谐振运动。一般说来,任何一个体系在稳定平衡点附近都可以近似地用线性谐振子来表示。在经典力学中,线性谐振子的运动是简谐运动。
基本介绍
- 中文名:线性谐振子
- 外文名:linear harmonic oscillator
- 定义:物理学中一个重要的模型
- 套用学科:量子力学术语
- 範畴:理工科
- 涉及:哈密顿量
概述
如果在一维空间内运动的粒子势能为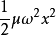 ,
,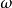 是常量,则这种体系就称为线性谐振子。这个问题的重要性在于许多体系都可以近似地看作是线性谐振子。例如,双原子分子中两原子之间的势能
是常量,则这种体系就称为线性谐振子。这个问题的重要性在于许多体系都可以近似地看作是线性谐振子。例如,双原子分子中两原子之间的势能 是两原子间距离
是两原子间距离 的函式,其形状如图1所示。
的函式,其形状如图1所示。
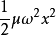
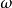


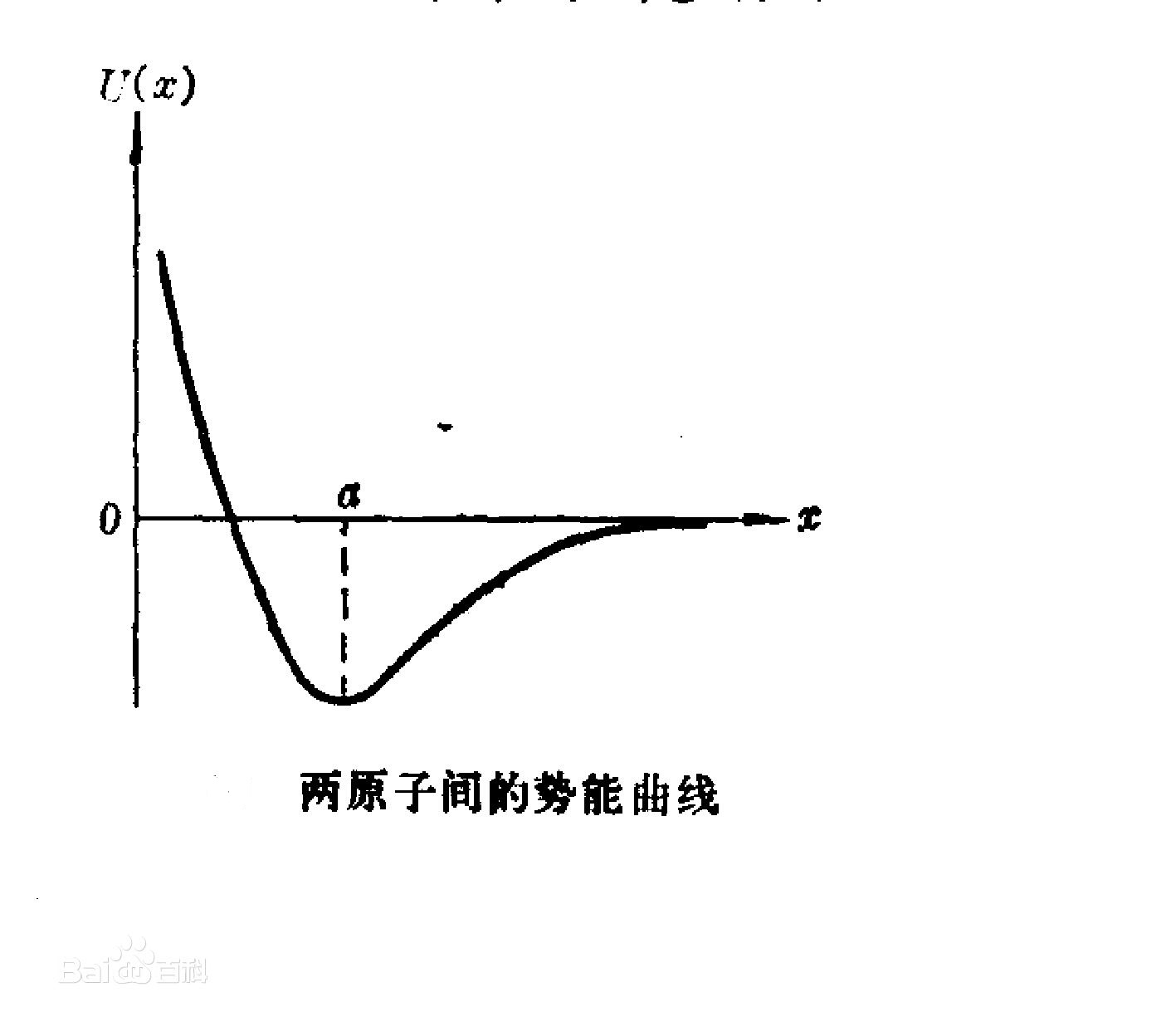 图1
图1在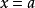 处,势能有一极小值,这是一个稳定平衡点。在这点附近,
处,势能有一极小值,这是一个稳定平衡点。在这点附近, 可以展成
可以展成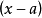 的幂级数,又因为在
的幂级数,又因为在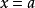 处,
处,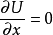 ,所以
,所以 可以近似地写成:
可以近似地写成: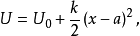 式中
式中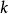 和
和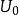 都是常量。这正是线性谐振子的势能。一般说来,任何一个体系在稳定平衡点附近都可以近似地用线性谐振子来表示。
都是常量。这正是线性谐振子的势能。一般说来,任何一个体系在稳定平衡点附近都可以近似地用线性谐振子来表示。
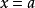

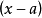
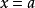
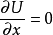

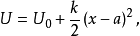
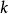
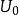
在经典力学中,线性谐振子的运动是简谐运动。势能为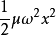 的线性谐振子,其坐标与时间的关係是
的线性谐振子,其坐标与时间的关係是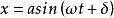 ,
, 是振幅,
是振幅,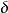 是初相。
是初相。
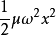
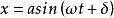

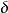
基本原理
线性谐振子是物理学中一个重要的模型,许多在平衡点附近振动的物理问题都可简化为线性谐振运动。在经典理论中质量为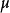 、距离平衡点位置为
、距离平衡点位置为 、振动频率为
、振动频率为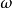 的线性谐振子,其总能量为:
的线性谐振子,其总能量为: