线性插值是指插值函式为一次多项式的插值方式,其在插值节点上的插值误差为零。线性插值相比其他插值方式,如抛物线插值,具有简单、方便的特点。线性插值的几何意义即为概述图中利用过A点和B点的直线来近似表示原函式。线性插值可以用来近似代替原函式,也可以用来计算得到查表过程中表中没有的数值。
基本介绍
- 中文名:线性插值
- 外文名:Linear Interpolation
- 定义:插值函式为一次多项式的插值方式
- 特点:简单、方便
- 几何意义:用过两插值节点的直线近似原函式
- 套用:近似代替原函式、插值得到数值
基础知识
已知函式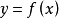 在区间
在区间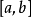 上
上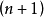 个互异点
个互异点 上的函式值
上的函式值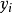 ,若存在一简单函式
,若存在一简单函式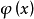 ,使
,使
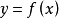
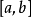
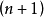

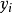
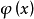
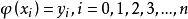
并要求误差
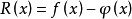
的绝对值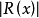 在整个区间
在整个区间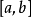 上比较小。这样的问题称为插值问题。
上比较小。这样的问题称为插值问题。
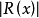
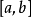
其中

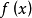
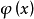
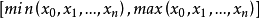
如果在插值区间内部用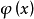 代替
代替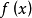 则称为内插;在插值区间以外,用
则称为内插;在插值区间以外,用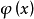 代替
代替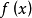 则称为外插。
则称为外插。
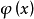
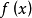
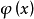
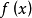
简介
线性插值是一种较为简单的插值方法,其插值函式为一次多项式。线性插值,在各插值节点上插值的误差为0。
如概述图中所示,设函式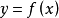 在两点
在两点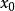 ,
,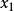 上的值分别为
上的值分别为 ,
,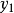 ,求多项式
,求多项式
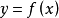
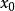
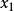

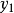
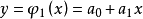
使满足
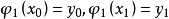
由解析几何可知
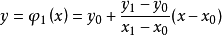
称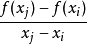 为
为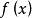 在
在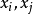 处的一阶均差,记以
处的一阶均差,记以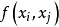 。于是,得
。于是,得
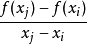
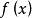
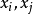
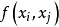
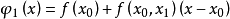
如果按照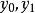 整理,则
整理,则
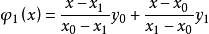
以上插值多项式为一次多项式,这种插值称为线性插值。
几何意义
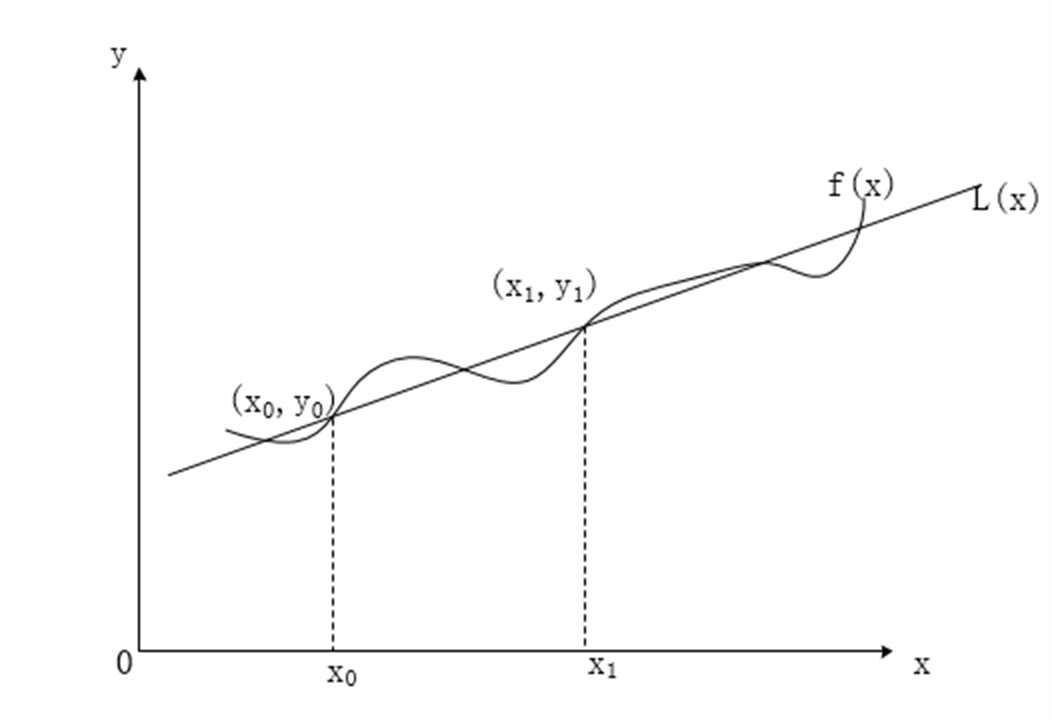
线性插值的几何意义如右图所示,即为利用过点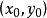 和
和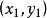 的直线
的直线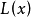 来近似原函式
来近似原函式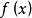 。
。
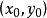
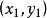
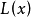
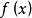

套用
1)线性插值在一定允许误差下,可以近似代替原来函式;
2)在查询各种数值表时,可通过线性插值来得到表中没有的数值。

