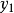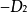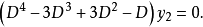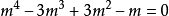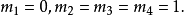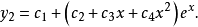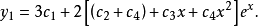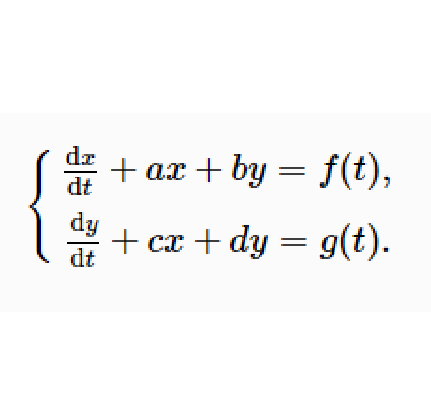线性微分方程组(first order linear differentialequation system)是由几个微分方程联立起来共同确定几个具有同一自变数的函式的情形.这些联立的微分方程称为微分方程组。
基本介绍
- 中文名:线性微分方程组
- 外文名:Linear Differential Equations
- 所属学科:数学
- 相关概念:线性微分方程、线性方程等
定义
线性微分方程组是具有完整构造性质和广泛套用的一类常微分方程组,如果方程组
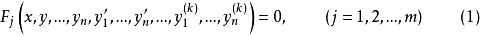
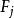
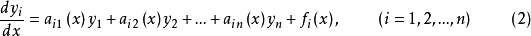
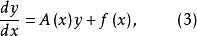
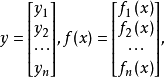
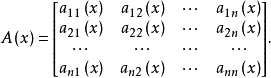
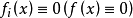

注意点: 一般地,线性微分方程组均可化为一阶线性微分方程组的典则形式。
一阶线性微分方程组
因为常微分方程的所有数值算法都是以一阶微分方程组为求解对象的,而任何阶的常微分方程都可转化为一阶微分方程组的形式,故需要学习一阶微分方程组的解法。可使用求解代数方程组的高斯消元法求解一阶微分方程组。
高斯消元法是求解线性方程组直接法中最常用和最有效的方法之一,其基本思想就是逐次消去一个未知数,使方程变换为一个等价方程组,然后求解该等价方程组,通过回代得到的解,再求解原方程的解。下面以例题介绍一阶线性微分方程组的解法。
例题1 解一阶微分方程组。
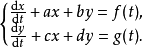
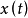
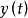
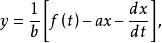
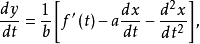
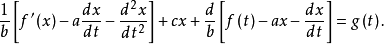
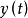
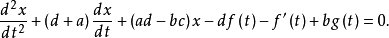
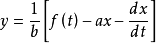
高阶常係数线性微分方程组
常係数线性微分方程组的求法:
(1)从方程组中消去一些未知函式及其各阶导数,得到只含有一个未知函式的高阶常係数线性微分方程。
(2)解此高阶微分方程,求出满足该方程的未知函式。
(3)把已求得的函式代入原方程组,一般来说。不必经过积分就可求出其余的未知函式。
例题2 解方程组
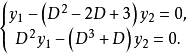
解:用消元法求解该方程组,消去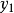 较为简便。用
较为简便。用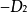 乘第一个式子与第二个式子相加,得
乘第一个式子与第二个式子相加,得