线性常微分方程是微分方程中出现的未知函式和该函式各阶导数都是一次的，称为线性常微分方程。它的理论是常微分方程理论中基本上完整、在实际问题中套用很广的一部份。
基本介绍
- 中文名：线性常微分方程
- 外文名：Linear ordinary differential equations
- 用途：在实际问题中套用很广的一部份
- 分类：线性常微分方程
- 学科：数理科学
定义
一阶线性微分方程的多种解法及其教学问题：
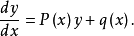
对应的齐次线性方程为 ：
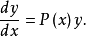
微分方程
欲得到非齐次线性微分方程的通解，我们首先求出对应的齐次方程的通解，然后用待定係数法或常数变易法求出非齐次方程本身的一个特解，把它们相加，就是非齐次方程的通解。
待定係数法
考虑以下的微分方程：
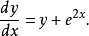
对应的齐次方程是：
它的通解是：
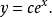
由于非齐次的部分是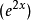
，我们猜测特解的形式是：
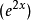
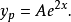
把这个函式以及它的导数代入微分方程中，我们可以解出A：
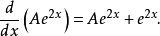
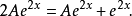
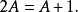
因此，原微分方程的解是：
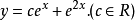
常数变易法
假设有以下的微分方程：
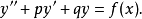
我们首先求出对应的齐次方程的通解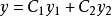
，其中C1、C2是常数，y1、y2是x的函式。然后我们用常数变易法求出非齐次方程的一个特解，方法是把齐次方程的通解中的常数C1、C2换成x的未知函式u1、u2，也就是：
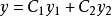
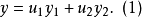
两边求导数，可得：
我们把函式u1、u2加上一条限制：
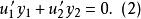
于是：
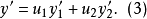
两边再求导数，可得：
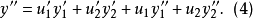
把(1)、(3)、(4)代入原微分方程中，可得：
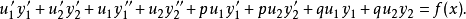
整理，得：
由于y1和y2都是齐次方程的通解，因此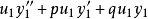
和
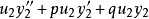都变为零，故方程化为：
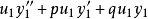
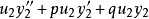
(2)和(5)联立起来，便得到了一个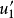
和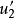
的方程组，便可得到
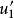和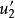
的表达式；再积分，便可得到
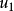和
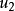的表达式。
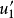
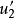
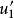
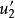
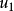
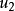
这个方法也可以用来解高于二阶的非齐次线性微分方程。一般地，有：
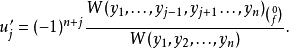
其中W表示朗斯基行列式。